【题目】将一块直角三角板![]() 放置在锐角
放置在锐角![]() 上,使得该三角板的两条直角边
上,使得该三角板的两条直角边![]() 恰好分别经过点
恰好分别经过点![]()
(1)如图①,若![]() 时,点
时,点![]() 在
在![]() 内,则
内,则![]() 度,
度,![]() ____度,
____度,![]() 度;
度;
(2)如图②,改变直角三角板![]() 的位置,使点
的位置,使点![]() 在
在![]() 内,请探究
内,请探究![]() 与
与![]() 之间存在怎样的数量关系,并验证你的结论;
之间存在怎样的数量关系,并验证你的结论;
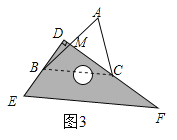
(3)如图③,改变直角三角板![]() 的位置,使点
的位置,使点![]() 在
在![]() 外,且在
外,且在![]() 边的左侧,直接写出
边的左侧,直接写出![]() 三者之间存在的数量关系.
三者之间存在的数量关系.

参考答案:
【答案】(1)135;90;45;(2)∠ABD+∠ACD=90°-∠A,证明见解析;(3)∠ACD-∠ABD=90°-∠A
【解析】
(1)在△BCD中,根据三角形内角和定理可得∠DBC+∠DCB =90°,在△ABC中,根据三角形内角和定理可得∠ABC+∠ACB=135°,进而可求出∠ABD+∠ACD的度数;
(2)根据三角形内角和定理可得∠ABC+∠ACB=180°-∠A,∠DBC+∠DCB=90°,
整理可得∠ABD+∠ACD=90°-∠A;
(3)根据三角形内角和定理可得∠ACD+∠A+∠AMC=180°,∠ABD+∠D+∠BMD=180°,整理可得∠ACD-∠ABD=90°-∠A.
解:(1)在△ABC中,∵∠A=45°,
∴∠ABC+∠ACB=180°-45°=135°,
在△DBC中,∵∠BDC=90°,
∴∠DBC+∠DCB=180°-90°=90°,
∴∠ABD+∠ACD=135°-90°=45°;
故答案为:135;90;45.
(2)∠ABD+∠ACD与∠A之间的数量关系为:∠ABD+∠ACD=90°-∠A.证明如下:
在△ABC中,∠ABC+∠ACB=180°-∠A.
在△DBC中,∠DBC+∠DCB=90°.
∴∠ABC+∠ACB-(∠DBC+∠DCB)=180°-∠A-90°.
∴∠ABD+∠ACD=90°-∠A.
(3)∠ACD-∠ABD=90°-∠A.
如图③,设AB交CD于点M,
∵∠ACD+∠A+∠AMC=180°,∠ABD+∠D+∠BMD=180°,∠AMC=∠BMD,
∴∠ACD-∠ABD=90°-∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学在一次实验中统计了某一结果出现的频率,给出的统计图如图所示,则 符合这一结果的实验可能是( )

A. 掷一枚正六面体的骰子,出现6点的概率
B. 掷一枚硬币,出现正面朝上的概率
C. 任意写出一个整数,能被2整除的概率
D. 一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程(组):
(1)
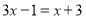
(2)
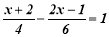
(3)
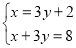
(4)
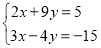
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在五一期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且余30个座位.
(1)求外出旅游的学生人数是多少,单租45座的客车需多少辆?
(2)已知45座的客车每辆租金250元,60座的客车每辆租金300元,为节省租金,并且保证每个学生都有座,决定同时租用两种客车,使得租车总数比单租45座的客车少一辆,问45座的客车和60座的客车分别租多少辆才能使得租金最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣
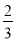 x2
x2【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣
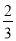 ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣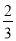 x2.
x2.考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计解析,绘制了如下不完整的统计表和统计图(图).
次数
10
8
6
5
人数
3
a
2
1
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中任选一人向学校汇报义工活动情况,参加了10次活动的成员被选中的概率有多少?

相关试题

