【题目】已知抛物线y=﹣![]() x2+bx+4与x轴相交于AB两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于AB两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
(1)求抛物线的表达式及它的对称轴方程;
(2)求点C的坐标,并求线段BC所在直线的函数表达式;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线解析式为 ![]() 对称轴方程为:
对称轴方程为:![]() ;(2)点C的坐标为(0,4),直线BC的解析式为
;(2)点C的坐标为(0,4),直线BC的解析式为![]() ;(3)存在点Q,使
;(3)存在点Q,使![]() 为等腰三角形,点Q的坐标为:
为等腰三角形,点Q的坐标为:![]()
![]() .
.
【解析】
试题分析:(1)利用待定系数法求出抛物线解析式,利用配方法或公式法![]() 求出对称轴方程;
求出对称轴方程;
在抛物线解析式中,令![]() ,可求出点C的坐标,令
,可求出点C的坐标,令![]() ,可求出点B的坐标,再利用待定系数法求出直线BC的解析式;
,可求出点B的坐标,再利用待定系数法求出直线BC的解析式;
本问为存在型问题.若![]() 为等腰三角形,则有三种可能的情况,需要分类讨论,逐一计算.
为等腰三角形,则有三种可能的情况,需要分类讨论,逐一计算.
试题解析:
∵抛物线![]() 的图象经过点A(-2,0),
的图象经过点A(-2,0),![]() ,解得
,解得![]()
∴抛物线解析式为 ![]() 又∵
又∵![]() ∴对称轴方程为:
∴对称轴方程为:![]()
(2)在![]() 中,令
中,令![]() ,得
,得![]() ,∴C(0,4);令
,∴C(0,4);令![]() ,即
,即![]() ,整理得
,整理得![]() 解得:
解得:![]() ∴A(-2,0),B(8,0).设直线BC的解析式为
∴A(-2,0),B(8,0).设直线BC的解析式为![]() ,把B(8,0),C(0,4)的坐标分别代入解析式,得:
,把B(8,0),C(0,4)的坐标分别代入解析式,得:![]() ,解得
,解得 ,直线BC的解析式为
,直线BC的解析式为![]()
(3)∵抛物线的对称轴方程为:![]() 可设点Q(3,t),则可求得:
可设点Q(3,t),则可求得:![]()
![]()
![]() ①当
①当![]() 时,有
时,有![]() 解得
解得![]() ∴
∴![]() ②当
②当![]() 时,有
时,有![]() 此方程无实数根,∴此时
此方程无实数根,∴此时![]() 不能构成等腰三角形;当
不能构成等腰三角形;当![]() 时,有
时,有![]() 解得:
解得:![]() ∴点Q坐标为:
∴点Q坐标为:![]() .综上所述,存在点Q,使
.综上所述,存在点Q,使![]() 为等腰三角形,点Q的坐标为:
为等腰三角形,点Q的坐标为:![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在第二象限,若该点到x轴的距离为3,到y轴的距离为1,则点P的坐标是( )
A. (﹣1,3) B. (﹣3,1) C. (3,﹣1) D. (1,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
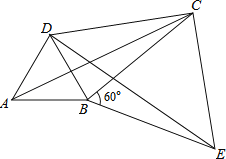
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2-4x-3=0时,配方后得到的方程为( ).
A.(x+2)2=0 B.(x-2)2=0 C.(x+2)2=2 D.(x-2)2=7
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a+a3=a4 B.(4a)3=12a3 C.a8÷a2=a4 D.a2a3=a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(﹣3,5)所在象限为( )
A. 第一象限 B. 第二象限 C. 第三象 D. 第四象限
相关试题

