【题目】给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
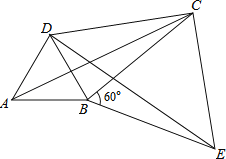
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
参考答案:
【答案】(1)(2)证明见解析
【解析】
试题分析:(1)根据定义和特殊四边形的性质,则有矩形或正方形或直角梯形;
(2)①首先证明△ABC≌△DBE,得出AC=DE,BC=BE,连接CE,进一步得出△BCE为等边三角形;
②利用等边三角形的性质,进一步得出△DCE是直角三角形,问题得解.
解:(1)正方形、矩形、直角梯形均可;
证明:(2)①∵△ABC≌△DBE,
∴BC=BE,
∵∠CBE=60°,
∴△BCE是等边三角形;
②∵△ABC≌△DBE,
∴BE=BC,AC=ED;
∴△BCE为等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
在Rt△DCE中,
DC2+CE2=DE2,
∴DC2+BC2=AC2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+4x+3的图象的对称轴为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在第二象限,若该点到x轴的距离为3,到y轴的距离为1,则点P的坐标是( )
A. (﹣1,3) B. (﹣3,1) C. (3,﹣1) D. (1,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣
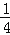 x2+bx+4与x轴相交于AB两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于AB两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).(1)求抛物线的表达式及它的对称轴方程;
(2)求点C的坐标,并求线段BC所在直线的函数表达式;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2-4x-3=0时,配方后得到的方程为( ).
A.(x+2)2=0 B.(x-2)2=0 C.(x+2)2=2 D.(x-2)2=7
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a+a3=a4 B.(4a)3=12a3 C.a8÷a2=a4 D.a2a3=a5
相关试题

