【题目】已知在等边三角形![]() 的三边上,分别取点
的三边上,分别取点![]() .
.
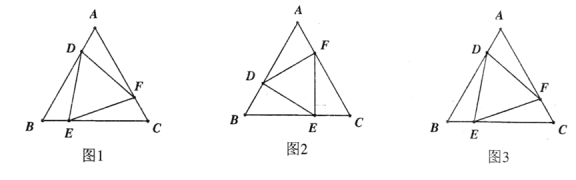
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() 于点
于点![]() 于
于![]() 于
于![]() ,且
,且![]() ,求
,求![]() 的长;
的长;
(3)如图3,若![]() ,求证:
,求证:![]() 为等边三角形.
为等边三角形.
参考答案:
【答案】(1)证明见解析;(2)5;(3)证明见解析.
【解析】
(1)根据等边三角形的性质得出![]() ,
,![]() ,
,![]() ,进一步证得
,进一步证得![]() ,即可证得
,即可证得![]() ;
;
(2)根据等边三角形性质和30°的直角三角形性质,得出线段长之间关系,列出方程即可解答;
(3)延长BD到M,使BM=AD,连接ME,延长EC到N,使CN=BE,连接FN,可得![]() ,再证
,再证![]() ,从而得出
,从而得出![]() ,再由三角形外角性质即可证得结论.
,再由三角形外角性质即可证得结论.
证明:(1)如图1中,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
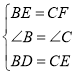 ,
,
∴![]() ,
,
(2)如图2中,![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
同理可得:![]() ,
,![]() ,
,
∵![]() ,即:
,即:![]()
∴![]()
解得:![]()
(3)如图3,延长BD到M,使BM=AD,连接ME,延长EC到N,使CN=BE,连接FN,
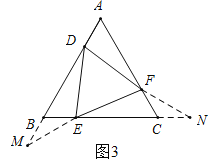
∵AD=CF,
∴BM=CF,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
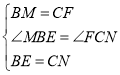 ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]()
在![]() 和
和![]() 中,
中,
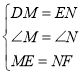 ,
,
![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ;
;
又∵![]()
∴![]() 为等边三角形.
为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
(2)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用a、b、c作三角形的三边,其中不能构成直角三角形的是( )
A. a2=(b+c)(b﹣c) B. a:b:c=1:
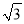 :2
:2C. a=32,b=42,c=52 D. a=5,b=12,c=13
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为
 ,求线段EF的长.
,求线段EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在学习绝对值后,我们知道,|a|表示数a在数轴上的对应点与原点的距离.如:|5|表示5在数轴上的对应点到原点的距离.而|5|=|5﹣0|,即|5﹣0|也可理解为5、0在数轴上对应的两点之间的距离.类似的,|5-3|表示5与3之差的绝对值,也可理解为5与3两数在数轴上所对应的两点之间的距离.如|x-3|的几何意义是数轴上表示有理数3的点与表示数x的点之间的距离,一般地,点A、B在数轴上分别表示数a、b,那么A、B之间的距离可表示为|a﹣b|.
请根据绝对值的意义并结合数轴解答下列问题:
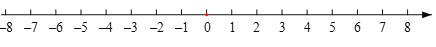
(1)数轴上表示2和3的两点之间的距离是 ;数轴上表示数a的点与表示﹣2的点之间的距离表示为 ;
(2)数轴上点P表示的数是2,P、Q两点的距离为3,则点Q表示的数是 ;
(3)数轴上有一个点表示数a,则|a+1|+|a-3|+|a+8|的最小值为 ;
(4)a、b、c、d在数轴上的位置如下图所示,若|a-d|=12,|b-d|=7,|a-c|=9,则|b-c|等于 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阳泉市郊区教科局提出开展“三有课堂”,某中学在一节体现“三有课堂”公开展示课上,李老师展示一幅图,条件是:C为直线AB上一点,∠DCE为直角,CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,各个小组经过讨论后得到以下结论:①∠ACF与∠BCH互余 ②∠FCG与∠HCG互补 ③∠ECF与∠GCH互补 ④∠ACD﹣∠BCE=90°,聪明的你认为哪些组的结论是正确的,正确的有( )个.
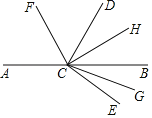
A.1B.2C.3D.4
相关试题

