【题目】如图,已知∠AOB以O为圆心,以任意长为半径作弧,分别交OA、OB于F、E两点,再分别以E、F为圆心,大于 ![]() EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.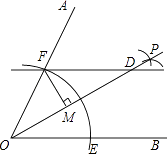
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证:△FMO≌△FMD.
参考答案:
【答案】
(1)解:∵OB∥FD,
∴∠0FD+∠A0B=18O°,
又∵∠0FD=116°,
∴∠A0B=180°﹣∠0FD=180°﹣116°=64°,
由作法知,0P是∠A0B的平分线,
∴∠D0B= ![]() ∠A0B=32°
∠A0B=32°
(2)证明:∵0P平分∠A0B,
∴∠A0D=∠D0B,
∵0B∥FD,
∴∠D0B=∠ODF,
∴∠A0D=∠ODF,
又∵FM⊥0D,
∴∠OMF=∠DMF,
在△MFO和△MFD中 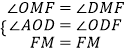 ,
,
∴△MFO≌△MFD(AAS).
【解析】(1)由作图的步骤可知是角平分线的作图,利用角平分线的性质及平行线的性质,再利用等腰三角形的内角和定理,可求出∠DOB度数;(2)利用平行线的内错角相等及角平分线条件,再利用已知,可根据“AAS”证出全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图:
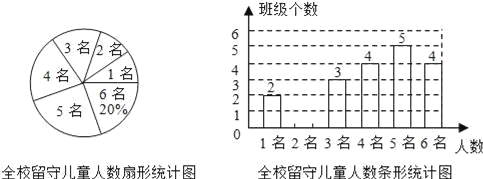
(1)将该条形统计图补充完整;
(2)求该校平均每班有多少名留守儿童?
(3)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果正确的是( )
A.3a﹣a=2
B.(a﹣b)2=a2﹣b2
C.6ab2÷(﹣2ab)=﹣3b
D.a(a+b)=a2+b -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:计算与化简,解分式方程
(1)aa5﹣(2a3)2+(﹣2a2)3
(2)先化简(a﹣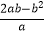 )
) 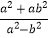 ,再求值,其中a=3,b=1
,再求值,其中a=3,b=1
(3)分解因式:(m﹣n)(3m+n)2+(m+3n)2(n﹣m)
(4)解分式方程: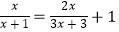 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句:
①对顶角相等
②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;
③过一点有且只有一条直线与已知直线平行,其中( )
A.①、②是正确的命题B.②、③是正确命题
C.①、③是正确命题D.以上结论皆错
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王在下面的计算中只做对了一道题,他做对的题目是( )
A.3a72a6=6a42
B.(a7)6=a42
C.a42÷a7=a6
D.a6+a6=a12 -
科目: 来源: 题型:
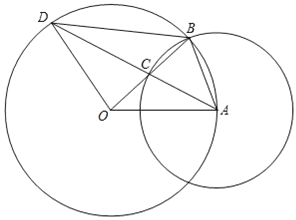
查看答案和解析>>【题目】如图,已知⊙O的半径OA的长为2,点B是⊙O上的动点,以AB为半径的⊙A与线段OB相交于点C,AC的延长线与⊙O相交于点D.设线段AB的长为x,线段OC的长为y.
(1)求y关于x的函数解析式,并写出定义域;
(2)当四边形ABDO是梯形时,求线段OC的长.
相关试题

