【题目】为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图:
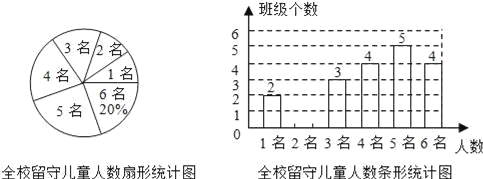
(1)将该条形统计图补充完整;
(2)求该校平均每班有多少名留守儿童?
(3)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
参考答案:
【答案】(1)见解析;(2)4;(3)![]() .
.
【解析】试题分析:(1)该校班级个数为4÷20%=20(个),只有2名留守儿童的班级个数为:20﹣(2+3+4+5+4)=2(个),补图如下:
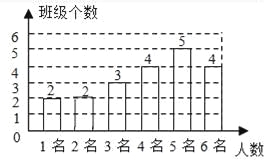
(2)该校平均每班留守儿童的人数为:(1×2+2×2+3×3+4×4+5×5+6×4)÷20=4(个);
(3)由(1)得只有2名留守儿童的班级有2个,共4名学生,设A1,A2来自一个班,B1,B2来自一个班,如图;
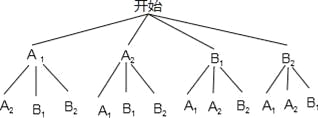
由树状图可知,共有12种可能的情况,并且每种结果出现的可能性相等,其中来自一个班的共有4种情况,则所选两名留守儿童来自同一个班级的概率为:![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明要从长度分别为5cm,6cm,11cm,16cm的四根小木棒中选出三根摆成一个三角形,那么他选的三根木棒形成的三角形的周长为( )cm
A.22B.27C.33D.32
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行
河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,
沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:
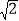 ≈1.41,
≈1.41,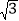 ≈1.73,结果保留整数)
≈1.73,结果保留整数)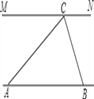
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(a,2 015)与点Q(2 016,b)关于x轴对称,那么a+b的值等于( )
A. -4031 B. -1 C. 1 D. 4031
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果正确的是( )
A.3a﹣a=2
B.(a﹣b)2=a2﹣b2
C.6ab2÷(﹣2ab)=﹣3b
D.a(a+b)=a2+b -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:计算与化简,解分式方程
(1)aa5﹣(2a3)2+(﹣2a2)3
(2)先化简(a﹣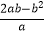 )
) 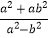 ,再求值,其中a=3,b=1
,再求值,其中a=3,b=1
(3)分解因式:(m﹣n)(3m+n)2+(m+3n)2(n﹣m)
(4)解分式方程: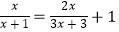 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB以O为圆心,以任意长为半径作弧,分别交OA、OB于F、E两点,再分别以E、F为圆心,大于
 EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.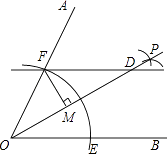
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证:△FMO≌△FMD.
相关试题

