【题目】如图,要建一个长方形养鸡场,养鸡场的一边靠墙(墙长25米),另三边用竹篱笆围成,竹篱笆的长为40米,若要围成的养鸡场的面积为180平方米,求养鸡场的宽各为多少米,设与墙平行的一边长为x米. 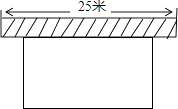
(1)填空:(用含x的代数式表示)另一边长为米;
(2)列出方程,并求出问题的解.
参考答案:
【答案】
(1)![]()
(2)解:设平行于墙的一边为x米,则另一边长为 ![]() 米,根据题意得:
米,根据题意得:
x ![]() =180,
=180,
整理得出:
x2﹣40x+360=0,
解得:x1=20+2 ![]() ,x2=20﹣2
,x2=20﹣2 ![]() ,
,
由于墙长25米,而20+2 ![]() >25,
>25,
∴x1=20+2 ![]() ,不合题意舍去,
,不合题意舍去,
∵0<20﹣2 ![]() <25,
<25,
∴x2=20﹣2 ![]() ,符合题意,
,符合题意,
此时 ![]() =10+
=10+ ![]() ,
,
答:此时鸡场靠墙的一边长(20﹣2 ![]() )米,宽是(10+
)米,宽是(10+ ![]() )米
)米
【解析】解:(1)设与墙平行的一边长为x米,另一边长为 ![]() 米, 故答案是:
米, 故答案是: ![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是按规律排列的一列数:
第1个式子:1-
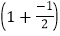 ;
;第2个式子:2-
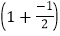 ×
×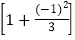 ×
×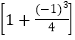 ;
;第3个式子:3-
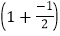 ×
×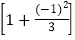 ×
×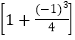 ×
×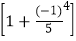 ×
×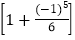 .
.(1)分别计算这三个式子的结果(直接写答案);
(2)写出第2018个式子的形式(中间部分用省略号,两端部分必须写详细),然后计算出结果.
-
科目: 来源: 题型:
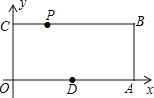
查看答案和解析>>【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B 运动.设 动点P的运动时间为t秒
(1)当t为何值时,四边形PODB是平行四边形?
(2)在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由。
(3) 在线段PB上有一点M,且PM=5,当P运动 秒时,四边形OAMP的周长最小, 并画图标出点M的位置。

-
科目: 来源: 题型:
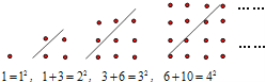
查看答案和解析>>【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10 …这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.用等式表示第100个正方形点阵中的规律_________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED的距离是11米,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
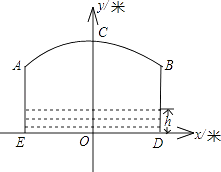
(1)根据题意,填空: ①顶点C的坐标为;
②B点的坐标为;
(2)求抛物线的解析式;
(3)已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系h=﹣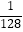 (t﹣19)2+8(0≤t≤40),且当点C到水面的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
(t﹣19)2+8(0≤t≤40),且当点C到水面的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
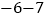 (2)
(2) 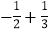
(3)
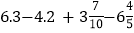 (4)
(4)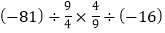
(5)
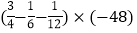 (6)-14+16÷(-2)3×|-3-1|
(6)-14+16÷(-2)3×|-3-1| -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的括号内
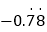 , -
, - , 0,
, 0, 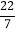 ,‐3.1415926, 20%, ‐3
,‐3.1415926, 20%, ‐3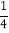 , 2, -1,3.1010010001…(每两个1之间逐次增加1个0)
, 2, -1,3.1010010001…(每两个1之间逐次增加1个0) ①正数集合{ ……}
②负数集合{ ……}
③整数集合{ ……}
④负分数集合{ ……}
⑤无理数集合{ ……}
相关试题

