搜索
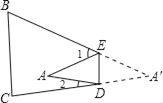
【题目】如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，
（1）设∠AED的度数为x，∠ADE的度数为y，那么∠1、∠2的度数分别是多少？（用含有x或y的代数式表示）
（2）∠A与∠1+∠2之间有一种数量关系始终保持不变，请找出这个规律，并说明理由．
参考答案：
【答案】（1）∠1＝（180﹣2x）度，∠2＝（180﹣2y）度；（2）∠A＝
（∠1+∠2）．
【解析】
（1）根据翻折不变性，得到∠AED=∠A′ED，∠ADE=∠A′DE，根据邻补角定义，可得到∠1、∠2的度数（用含有x或y的代数式表示）；
（2）根据（1）中结论和三角形的内角和定理即可求出∠A与∠1+∠2之间的数量关系．
（1）∵∠AED＝x度，∠ADE＝y度，
∴∠AEA′＝2x度，∠ADA′＝2y度，
∴∠1＝（180﹣2x）度，
∠2＝（180﹣2y）度；
（2）∵∠1＝（180﹣2x）度①，
∠2＝（180﹣2y）度②，
由①得，x＝（90﹣∠1），
由②得，y＝（90﹣∠2）．
∠A＝180﹣x﹣y＝180﹣（90﹣∠1）﹣（90﹣∠2）＝（∠1+∠2）度．
∴结论为：∠A＝（∠1+∠2）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们用
表示不大于
的最大整数，例如：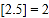
，
，
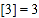；用
表示大于的最小整数，例如：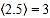
，
，
.解决下列问题：（1）
= ,，
= ；（2）若
=2，则
的取值范围是 ；若
=－1，则
的取值范围是 ；（3）已知
，满足方程组
，求，的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，对于任意三点A，B，C，给出如下定义： 如果矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的覆盖矩形．点A，B，C的所有覆盖矩形中，面积最小的矩形称为点A，B，C的最优覆盖矩形．例如，下图中的矩形A1B1C1D1 ， A2B2C2D2 ， AB3C3D3都是点A，B，C的覆盖矩形，其中矩形AB3C3D3是点A，B，C的最优覆盖矩形．
（1）已知A（﹣2，3），B（5，0），C（t，﹣2）． ①当t=2时，点A，B，C的最优覆盖矩形的面积为；
②若点A，B，C的最优覆盖矩形的面积为40，求直线AC的表达式；
（2）已知点D（1，1）．E（m，n）是函数y=
（x＞0）的图象上一点，⊙P是点O，D，E的一个面积最小的最优覆盖矩形的外接圆，求出⊙P的半径r的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】某健步走运动的爱好者用手机软件记录了某个月（30天）每天健步走的步数（单位：万步），将记录结果绘制成了如图所示的统计图．在每天所走的步数这组数据中，众数和中位数分别是（ ）
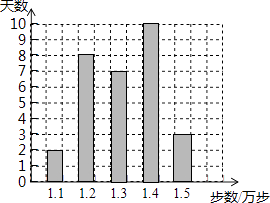
A.1.2，1.3
B.1.3，1.3
C.1.4，1.35
D.1.4，1.3 -
科目： 来源： 题型：
查看答案和解析>>【题目】图1是某娱乐节目中一个游戏环节的录制现场，场地由等边△ADE和正方形ABCD组成，正方形ABCD两条对角线交于点O，在AD的中点P处放置了一台主摄像机．游戏参与者行进的时间为x，与主摄像机的距离为y，若游戏参与者匀速行进，且表示y与x的函数关系式大致如图2所示，则游戏参与者的行进路线可能是（ ）
A.A→O→D
B.E→A→C
C.A→E→D
D.E→A→B -
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC请你按要求作图、解答（不写作法，但要保留作图痕迹）：
（1）用直尺和圆规，过点B作∠ABC的角平分线交AC于P；
（2）用直尺和直角三角板的直角画PD⊥AB、PE⊥BC垂足分别为D、E；
（3）用刻度尺分别量PD＝ cm和PE＝ cm．得PD PE（填大小关系）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD、AE分别是△ABC的高和角平分线，∠B＝30°，∠C＝70°，分别求：
（1）∠BAC的度数；
（2）∠AED的度数；
（3）∠EAD的度数．
相关试题
