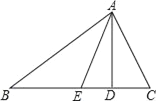
【题目】如图,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=70°,分别求:
(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
参考答案:
【答案】(1)80°;(2)70°;(3)20°.
【解析】
(1)根据三角形的内角和即可得到结论;
(2)根据角平分线的定义和三角形的内角和即可得到结论;
(3)根据极品飞车的定义和三角形的内角和即可得到结论.
(1)∵∠B=30°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=80°,
(2)∵AD为高,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=90°﹣70°=20°,
而AE为角平分线,
∴∠CAE=![]() ∠BAC=40°,
∠BAC=40°,
∴∠AED=90°﹣(∠CAE﹣∠CAD)=90°﹣(40°﹣20°)=70°;
(3)∵AE是△ABC的角平分线,
∴∠BAE=![]() ∠BAC=40°,
∠BAC=40°,
又∵AD⊥BC,
∴∠BAD=90°﹣∠B=60°,
∴∠EAD=∠BAD﹣∠BAE=60°﹣40°=20°.
-
科目: 来源: 题型:
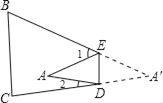
查看答案和解析>>【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)设∠AED的度数为x,∠ADE的度数为y,那么∠1、∠2的度数分别是多少?(用含有x或y的代数式表示)
(2)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是某娱乐节目中一个游戏环节的录制现场,场地由等边△ADE和正方形ABCD组成,正方形ABCD两条对角线交于点O,在AD的中点P处放置了一台主摄像机.游戏参与者行进的时间为x,与主摄像机的距离为y,若游戏参与者匀速行进,且表示y与x的函数关系式大致如图2所示,则游戏参与者的行进路线可能是( )

A.A→O→D
B.E→A→C
C.A→E→D
D.E→A→B -
科目: 来源: 题型:
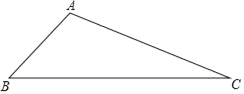
查看答案和解析>>【题目】已知△ABC请你按要求作图、解答(不写作法,但要保留作图痕迹):
(1)用直尺和圆规,过点B作∠ABC的角平分线交AC于P;
(2)用直尺和直角三角板的直角画PD⊥AB、PE⊥BC垂足分别为D、E;
(3)用刻度尺分别量PD= cm和PE= cm.得PD PE(填大小关系)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)
 =
= ﹣1
﹣1(2)10x+7=14x﹣5﹣3x
-
科目: 来源: 题型:
查看答案和解析>>【题目】小彬买了A、B两种书,单价分别是18元、10元.
(1)若两种书共买了10本付款172元,求每种书各买了多少本?
(2)买10本时付款可能是123元吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲沿周长为300米的环形跑道按逆时针方向跑步,速度为a米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.
(1)若a=1,求甲、乙两人第一次相遇所用的时间;
(2)若a>3,甲、乙两人第一次相遇所用的时间为80秒,试求a的值.

相关试题

