【题目】如图,在数轴上A点表示数-3,B点表示数b,C点表示数c,且b.c满足![]()
![]()
(1)b= ,c= .
(2)若使C.B两点的距离是A.B两点的距离的2倍,则需将点C向左移动 个单位长度.
(3)点A.B.C开始在数轴上运动,若点A以每秒m个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,设运动时间为t秒;
①点A.B.C表示的数分别是 . . (用含m.t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2,当m为何值时,2d1-d2的值不会随着时间t的变化而改变,并求出此时2d1-d2的值.
参考答案:
【答案】(1)b=-1,c=4;
(2) 1或9;
(3)①-3-mt;-1+2t;4+5t;②m=4;2d1-d2的值为12.
【解析】
(1)由![]() ,根据平方及绝对值的非负性可得b+1=0,c-4=0,据此可求得b、c的值;
,根据平方及绝对值的非负性可得b+1=0,c-4=0,据此可求得b、c的值;
;
(2)先求出AB和BC的长度,结合数轴即可得出点C向左移动的距离,有两解;
(3)①结合路程=时间×速度写出答案;
②根据①先表示出d1、d2,从而表示出2d1-d2,然后根据2d1-d2的值不会随着时间t的变化而改变得出t的系数为0,即可求出m的值,继而求出2d1-d2的值.
解:(1)∵![]()
∴b+1=0,c-4=0
∴b=-1,c=4
(2)由数轴可知:AB= 2,
∴B C=4,
∴点C向左移动后的数是3或-5
∴需将点C向左移动1或9个单位;
故答案是:1或9;
(3)①点A表示的数是-3-mt;点B表示的数是-1+2t;点C所表示的数是4+5t.
故答案是:-3-mt;-1+2t;4+5t;
②∵点A表示的数是-3-mt;点B表示的数是-1+2t;点C所表示的数是4+5,
∴d1=4+5t-(-1+2t)=3t+5,d2=-1+2t-(-3-mt)=(m+2)t+2,
∴2d1-d2=2(3t+5)-[(m+2)t+2]=(4-m)t+12,
∵2d1-d2的值不会随着时间t的变化而改变
∴4-m=0,
∴m=4,
故当m=4时,2d1-d2的值不会随着时间t的变化而改变,此时2d1-d2的值为12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A,B分别对应数a,b,其中a<0,b>0.
(1)当a=﹣2,b=6时,线段AB的中点对应的数是 ;(直接填结果)
(2)若该数轴上另有一点M对应着数m.
①当m=2,b>2,且AM=2BM时,求代数式a+2b+20的值;
②当a=﹣2,且AM=3BM时,请说明代数式3b﹣4m或2m﹣3b均有定值(不变的数值),并求出它们的定值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 分别是边
分别是边 的中点,延长
的中点,延长 到点
到点 ,使
,使 ,得四边形
,得四边形 .若使四边形
.若使四边形 是正方形,则应在
是正方形,则应在 中再添加一个条件为__________.
中再添加一个条件为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校“河南省汉子听写大赛初赛”冠军组成员的年龄分布
年龄/岁
12
13
14
15
人数
5
15
x
12﹣x
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A. 平均数、中位数 B. 平均数、方差 C. 众数、中位数 D. 中位数、方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列叙述正确的是( )
A. 符号不同的两个数是互为相反数
B. 一个有理数的相反数一定是负有理数
C. 2
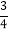 与2.75都是﹣
与2.75都是﹣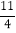 的相反数
的相反数D. 0没有相反数
-
科目: 来源: 题型:
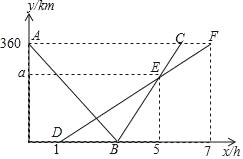
查看答案和解析>>【题目】快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)直接写出慢车的行驶速度和a的值;
(2)快车与慢车第一次相遇时,距离佳市的路程是多少千米?
(3)快车出发多少小时后两车相距为100km?请直接写出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=
 图象的两个交点.
图象的两个交点.(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣
 >0的解集.
>0的解集.
相关试题

