【题目】如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
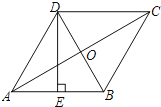
(1)求∠ABC的度数;
(2)如果![]() ,求DE的长.
,求DE的长.
参考答案:
【答案】(1)∠ABC=120°;(2)DE=2![]() .
.
【解析】
试题分析:(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,再根据菱形的四条边都相等可得AB=AD,然后求出AB=AD=BD,从而得到△ABD是等边三角形,再根据等边三角形的性质求出△DAB=60°,然后根据两直线平行,同旁内角互补求解即可;
(2)根据菱形的对角线互相平分求出AO,再根据等边三角形的性质可得DE=AO.
解:(1)∵E为AB的中点,DE⊥AB,
∴AD=DB,
∵四边形ABCD是菱形,
∴AB=AD,
∴AD=DB=AB,
∴△ABD为等边三角形.
∴∠DAB=60°.
∵菱形ABCD的边AD∥BC,
∴∠ABC=180°﹣∠DAB=180°﹣60°=120°,
即∠ABC=120°;
(2)∵四边形ABCD是菱形,
∴BD⊥AC于O,AO=![]() AC=
AC=![]() ×4
×4![]() =2
=2![]() ,
,
由(1)可知DE和AO都是等边△ABD的高,
∴DE=AO=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个蓄水池储水100 m3,用每分钟抽水0.5 m3的水泵抽水,则蓄水池的余水量y(m3)与抽水时间t(分)之间的函数关系式是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是某校九年级10名同学参加学校演讲比赛的统计表:
成绩/分
80
85
90
95
人数/人
1
2
5
2
则这组数据的中位数和平均数分别为( )
A. 90,90 B. 90,89 C. 85,89 D. 85,90
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,抛物线y=ax2+2x+c过点A、B且与y轴交与点C(0,3),点P为抛物线对称轴x=l上一动点.
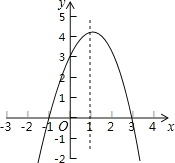
(1)求抛物线的解析式;
(2)求当AP+CP最小时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列表述,能确定位置的是( )
A. 银泰影院2排 B. 石家庄裕华路 C. 北偏东30° D. 东经118°,北纬40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上到表示-1的点的距离为4的点所表示的数是____________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形ABCD的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5.
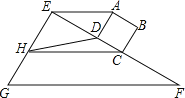
(1)当x=2时,AE的长为 ;
(2)试求出y关于x的函数关系式,并求出△EHD与△ADE的面积之差;
(3)当正方形ABCD移动时间x= 时,线段HD所在直线经过点B.
相关试题

