【题目】如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形ABCD的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5.
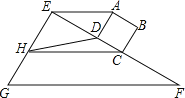
(1)当x=2时,AE的长为 ;
(2)试求出y关于x的函数关系式,并求出△EHD与△ADE的面积之差;
(3)当正方形ABCD移动时间x= 时,线段HD所在直线经过点B.
参考答案:
【答案】(1)![]() cm(2)
cm(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)根据正方形的性质得到∠ADE=90°,根据勾股定理计算即可;
(2)根据题意表示出EC=4﹣x,ED=3﹣x,证明△AED∽△HCE,根据相似三角形的性质得到比例式,代入计算即可;
(3)根据正方形的性质得到∠ADB=45°,根据等腰直角三角形的性质列出方程,解方程即可.
解:(1)当x=2时,即CF=2cm,
则EC=EF﹣CF=2cm,又CD=1cm,
∴ED=1cm,
∵四边形ABCD是正方形,
∴∠ADE=90°,
∴AE=![]() =
=![]() cm,
cm,
故答案为:![]() cm;
cm;
(2)∵正方形移动时间为x(s),
∴CF=x,
则EC=4﹣x,ED=3﹣x,
∵AE∥HC,
∴∠AED=∠HCE,又∠ADE=∠HEC,
∴△AED∽△HCE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,y=![]() ,
,
△ADE的面积=![]() ×(3﹣x)×1=
×(3﹣x)×1=![]() ,
,
△EHC的面积=![]() ×(4﹣x)×
×(4﹣x)×![]() =
=![]() ,
,
则△EHD的面积=![]() ×
×![]() ×
×![]() =
=![]() ,
,
△EHD的面积﹣△ADE的面积=![]() ;
;
(3)当线段HD所在直线经过点B时,
∵∠ADB=45°,∠ADE=90°,
∴∠EDH=45°,
∴EH=ED,即![]() =3﹣x,
=3﹣x,
解得,x1=![]() ,x2=
,x2=![]() (舍去),
(舍去),
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
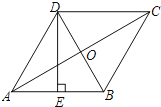
(1)求∠ABC的度数;
(2)如果
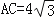 ,求DE的长.
,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列表述,能确定位置的是( )
A. 银泰影院2排 B. 石家庄裕华路 C. 北偏东30° D. 东经118°,北纬40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上到表示-1的点的距离为4的点所表示的数是____________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
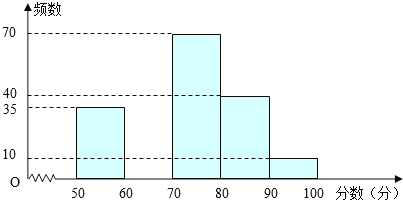
根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是( )
A. 第一次向右拐40, 第二次向左拐140
B. 第一次向左拐40, 第二次向右拐40
C. 第一次向左拐40, 第二次向左拐140
D. 第一次向右拐40, 第二次向右拐40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
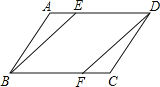
求证:(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.
相关试题

