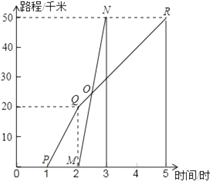
【题目】如图所示,A、B两地相距50千米,阿杜于某日下午1时骑自行车从A地出发驶往B地,浩浩也于同日下午骑摩托车按路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示阿杜和浩浩所行驶的路程S和时间t的关系:
根据图象回答下列问题:
(1)阿杜和浩浩哪一个出发的更早?早出发多长时间?
(2)浩浩骑摩托车的速度和阿杜骑自行车在全程的平均速度分别是多少?
(3)请你根据图象上的数据,求出浩浩出发用多长时间就追上阿杜?
参考答案:
【答案】(1)阿杜出发的更早,早出发1小时;(2)浩浩的速度 是50千米/小时,
阿杜的平均速度是12.5千米/小时;(3)0.5小时.
【解析】
(1)读图可知;
(2)从图中得:阿杜和浩浩所走的路程都是50千米,阿杜一共用了4小时,浩浩一共用了1小时,根据速度=![]() ,代入计算得出;
,代入计算得出;
(3)从图中得:阿杜在走完全程时,前1小时速度为20千米/小时,从第2小时开始,速度为![]() =10千米/小时,因此设浩浩出发x小时就追上甲,则从图中看,是在阿杜速度为10千米/小时时与浩浩相遇,所以阿杜的路程为20+10x,浩浩的路程为50x,列方程解出即可.
=10千米/小时,因此设浩浩出发x小时就追上甲,则从图中看,是在阿杜速度为10千米/小时时与浩浩相遇,所以阿杜的路程为20+10x,浩浩的路程为50x,列方程解出即可.
解:(1)阿杜下午1时出发,浩浩下午2时出发,
所以阿杜出发的更早,早出发1小时;
(2)浩浩的速度=![]() =50(千米/小时),
=50(千米/小时),
阿杜的平均速度=![]() =12.5(千米/小时);
=12.5(千米/小时);
(3)设浩浩出发x小时就追上阿杜,
根据题意得:50x=20+10x,
x=0.5,
答:浩浩出发0.5小时就追上阿杜.
故答案为:(1)阿杜出发的更早,早出发1小时;(2)浩浩的速度 是50千米/小时,
阿杜的平均速度是12.5千米/小时;(3)0.5小时.
-
科目: 来源: 题型:
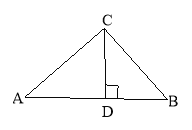
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB于点D,AC=4,BC=3,DB=
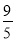 ,
,(1)求CD、AD的长
(2)判断△ABC的形状,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.例如:由图1可得到
 .
.
(1)写出由图2所表示的数学等式:________.

(2)写出由图3所表示的数学等式:________.

(3)已知实数
 ,
, ,
, 满足
满足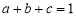 ,
, .
.①求
 的值.
的值.②求
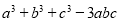 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).
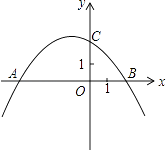
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A、C、D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;
(3)以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式. -
科目: 来源: 题型:
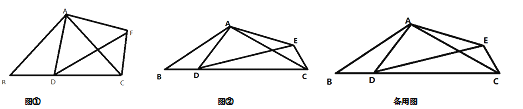
查看答案和解析>>【题目】已知如图,在△ABC中,AB=AC,点D是线段BC上一个动点,以AD为腰在线段AD的右侧作△ADE,且AD=AE。
(1)如图①,当∠BAC=∠DAE=90°时,试判断线段BD和CE有什么关系,并给出证明:
(2)在(1)的条件下,若BC=4.试判断四边形ADCE的面积是否发生变化,若不变,求出四边形ADCE的面积;若变化,请说明理由;
(3)如图②,若∠BAC=∠DAE=120°,BC=4,试探索△DCE的面积是否存在最大值,若存在,求出此时∠DEC的度数,若不存在,请说明理由。
-
科目: 来源: 题型:
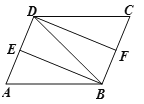
查看答案和解析>>【题目】如图,在□ABCD中,AB=DB,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DFBE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列代数式书写规范的是( )
A. a÷3B. a8C. 5aD.

相关试题

