【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.例如:由图1可得到![]() .
.

(1)写出由图2所表示的数学等式:________.

(2)写出由图3所表示的数学等式:________.

(3)已知实数![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() .
.
①求![]() 的值.
的值.
②求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①0 ;②1.
;(3)①0 ;②1.
【解析】
(1)根据数据表示出正方形的边长,再根据正方形的面积公式写出等式的左边,再表示出每一小部分的面积,然后根据面积相等即可写出等式;
(2)根据数据表示出阴影正方形的边长,再根据正方形的面积公式写出等式的左边,再用大正方形的面积减去其他八小部分的面积,然后根据面积相等即可写出等式;
(3)①根据(1)的结论变形为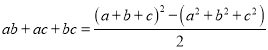 ,代数求值即可得解;
,代数求值即可得解;
②在①的基础上即可求得![]() 的值.
的值.
解:(1)∵大正方形的边长为![]()
∴大正方形的面积可表示为![]()
∵观察图形可知九小部分的面积和为![]()
![]()
∴由图2所表示的数学等式:![]() ;
;
(2)∵阴影正方形的边长为![]()
∴阴影正方形的面积为![]()
∵阴影正方形的面积还以表示为大正方形的面积减去其他八小部分的面积:
![]()
∴由图3所表示的数学等式:![]() ;
;
(3)①∵由图2所表示的数学等式:![]()
∴![]()
∴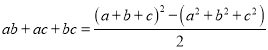
∵![]() ,
,![]()
∴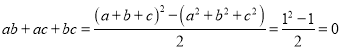 ,即
,即![]() ;
;
②∵![]() ,
,![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
(1)k的值是;
(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=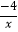 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若
图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 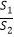 =
=  ,则b的值是 .
,则b的值是 . 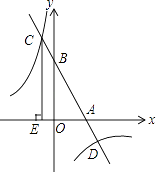
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.
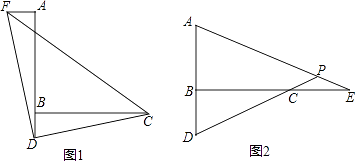
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由. -
科目: 来源: 题型:
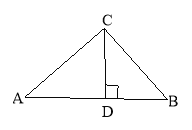
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB于点D,AC=4,BC=3,DB=
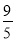 ,
,(1)求CD、AD的长
(2)判断△ABC的形状,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).
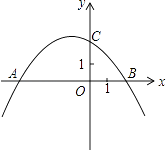
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A、C、D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;
(3)以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式. -
科目: 来源: 题型:
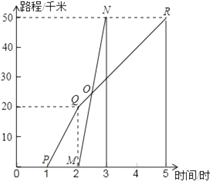
查看答案和解析>>【题目】如图所示,A、B两地相距50千米,阿杜于某日下午1时骑自行车从A地出发驶往B地,浩浩也于同日下午骑摩托车按路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示阿杜和浩浩所行驶的路程S和时间t的关系:
根据图象回答下列问题:
(1)阿杜和浩浩哪一个出发的更早?早出发多长时间?
(2)浩浩骑摩托车的速度和阿杜骑自行车在全程的平均速度分别是多少?
(3)请你根据图象上的数据,求出浩浩出发用多长时间就追上阿杜?
-
科目: 来源: 题型:
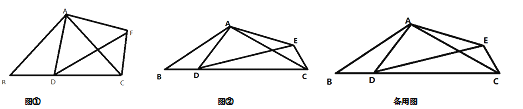
查看答案和解析>>【题目】已知如图,在△ABC中,AB=AC,点D是线段BC上一个动点,以AD为腰在线段AD的右侧作△ADE,且AD=AE。
(1)如图①,当∠BAC=∠DAE=90°时,试判断线段BD和CE有什么关系,并给出证明:
(2)在(1)的条件下,若BC=4.试判断四边形ADCE的面积是否发生变化,若不变,求出四边形ADCE的面积;若变化,请说明理由;
(3)如图②,若∠BAC=∠DAE=120°,BC=4,试探索△DCE的面积是否存在最大值,若存在,求出此时∠DEC的度数,若不存在,请说明理由。
相关试题

