【题目】如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.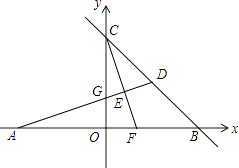
(1)求D点的坐标;
(2)求证:OF=OG;
(3)在第一象限内是否存在点P,使得△CFP为等腰直角三角形?若存在,请求出点P的坐标,若不存在,请说明理由.
参考答案:
【答案】
(1)
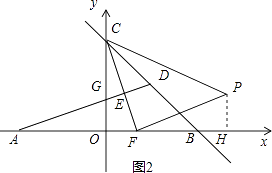
解:如图1,作DH⊥x轴于H,
∵OA=OB=OC=4,
∴AB=8,B(4,0),C(0,4),
设BC的解析式为y=kx+b,
把B,C两点代入得 ![]() ,解得:
,解得: ![]() ,
,
∴BC的解析式为y=﹣x+4,
∵△ABD的面积为8,AB=8,
∴DH=2,
所以D点的纵坐标为2,
把y=2代入y=﹣x+4得:x=2,
∴D(2,2);
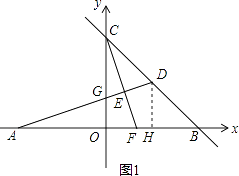
(2)
解:∵CE⊥AD,
∴∠CEG=∠AOG=90°,
又∵∠AGO=∠CGE,
∴△AGO~△CGE,
∴∠GAO=∠GCE,
在△COF与△AOG中, 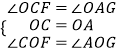 ,
,
∴△COF≌△AOG,
∴OF=OG;
(3)
解:存在,∵A(﹣4,0),D(2,2),
∴直线AD的解析式为y= ![]() x+
x+ ![]() ,
,
∴OG= ![]() ,
,
∴OF=OG= ![]() ,
,
①如图2,当∠CFP=90°,FP=FC时,
过P作PH⊥x轴于H,
∴∠PHF=∠COF=90°,
∴∠OCF+∠OFC=∠OFC+∠PFH=90°,∴∠OCF=∠PFH,
在△COF与△PFH中, 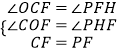 ,∴△COF≌△PFH,∴PH=OF=
,∴△COF≌△PFH,∴PH=OF= ![]() ,FH=OC=4,
,FH=OC=4,
∴OH= ![]() ,
,
∴P1( ![]() ,
, ![]() );
);
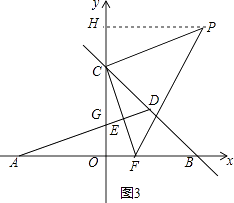
②如图3,当∠PCF=90°,CP=FC时,同理证得△PHC≌△CFO,
∴PH=OC=4,CH=OF= ![]() ,
,
∴OH= ![]() ,
,
∴P2(4, ![]() );
);
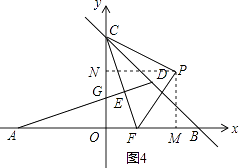
③如图4,当∠CPF=90°,PC=PF时,
过P作PM⊥x轴于M,PN⊥y轴于N,
∴四边形PNOM是矩形,
∴∠NPM=90°,
∴∠CPN+∠NPF=∠NPF+∠FPM=90°,
∴∠CPN=∠FPM,
在△CPN与△FPM中, 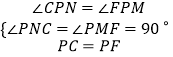 ,
,
∴△PNC≌△PMF,
∴PN=PM,CN=FM,
∴矩形PNOM是正方形,
∴ON=OM,
∴4﹣CN= ![]() +CN,
+CN,
∴CN=CM= ![]() ,
,
∴PN=PM= ![]() ,
,
∴P3( ![]() ,
, ![]() ),
),
综上所述:P的坐标为( ![]() ,
, ![]() ),(4,
),(4, ![]() ),(
),( ![]() ,
, ![]() ).
).
【解析】(1)根据已知条件得到AB=8,B(4,0),C(0,4),待定系数法求得BC的解析式为y=﹣x+4,根据三角形的面积得到DH=2,即可得到结论;(2)根据已知条件得到△AGO~△CGE,由相似三角形的性质得到∠GAO=∠GCE,根据全等三角形的性质即可得到结论;(3)根据直线AD的解析式y= ![]() x+
x+ ![]() ,求得OF=OG=
,求得OF=OG= ![]() ,①如图2,当∠CFP=90°,FP=FC时,过P作PH⊥x轴于H,根据全等三角形的性质得到PH=OF=
,①如图2,当∠CFP=90°,FP=FC时,过P作PH⊥x轴于H,根据全等三角形的性质得到PH=OF= ![]() ,FH=OC=4,于是得到P1(
,FH=OC=4,于是得到P1( ![]() ,
, ![]() );②如图3,当∠PCF=90°,CP=FC时,根据全等三角形的性质得到PH=OC=4,CH=OF=
);②如图3,当∠PCF=90°,CP=FC时,根据全等三角形的性质得到PH=OC=4,CH=OF= ![]() ,于是得到P2(4,
,于是得到P2(4, ![]() );③如图4,当∠CPF=90°,PC=PF时,根据全等三角形的性质得到PN=PM,CN=FM,根据ON=OM,列方程得到CN=CM=
);③如图4,当∠CPF=90°,PC=PF时,根据全等三角形的性质得到PN=PM,CN=FM,根据ON=OM,列方程得到CN=CM= ![]() ,于是得到P3(
,于是得到P3( ![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】浙江省统计局发布的数据显示,2018年末,全省常住人口为5737万人.数据“5737万”用科学记数法表示为( )
A.5737×l04B.57.37×106C.5.737×107D.5.737×108
-
科目: 来源: 题型:
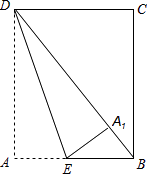
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,CD=12,BC=15,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A1处,求AE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途经C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
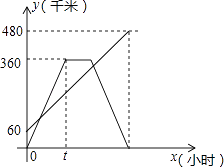
(1)乙车的速度是千米/时,t=小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3x3﹣27x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年,我国一些地区遭受旱灾,旱灾牵动全国人民的心.图(1)是我市某中学“献爱心,抗旱灾”自愿捐款活动中学生捐款情况制成的条形统计图,图(2)是该中学学生人数比例分布(已知该校共有学生1450人).
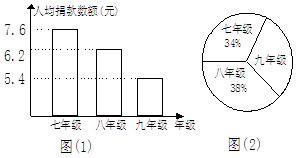
(1)初三学生共捐款多少元?
(2)该校学生平均每人捐款多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算.
(1)(﹣2.8)+7.2+5.5+(﹣4.2)
(2)(﹣7)﹣(﹣10)+(﹣8)﹣(﹣2)
(3)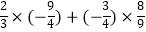
(4)﹣72×2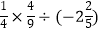
(5)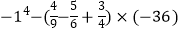
(6)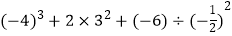 .
.
相关试题

