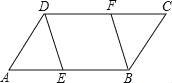
【题目】在ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.
参考答案:
【答案】证明见解析
【解析】
试题分析:(1)首先根据平行四边形的性质可得AD=BC,∠A=∠C,再加上条件AE=CF可利用SAS证明△ADE≌△CBF;
(2)首先证明DF=BE,再加上条件AB∥CD可得四边形DEBF是平行四边形,又DF=FB,可根据邻边相等的平行四边形为菱形证出结论.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
∵在△ADE和△CBF中,
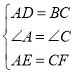 ,
,
∴△ADE≌△CBF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴DF=EB,
∴四边形DEBF是平行四边形,
又∵DF=FB,
∴四边形DEBF为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不等式变形正确的是( )
A.若a>b,则a﹣2>b﹣2
B.若- ?a<2,则a<﹣4
?a<2,则a<﹣4
C.若a>b,则1﹣2a>1﹣2b
D.若a<b,则ac2<bc2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2-ab=8,ab-b2=-4,则a2-2ab+b2=_______.
-
科目: 来源: 题型:
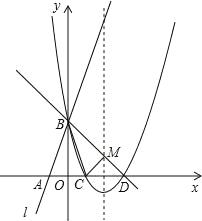
查看答案和解析>>【题目】如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
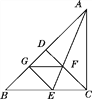
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于点F,交BC于点E,过点E作EG⊥AB于G,连结GF.求证:四边形CFGE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个开口向上,并且对称轴为直线x=1的抛物线的表达式y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四边形中,对角线相等且互相垂直平分的是( )
A. 平行四边形 B. 正方形 C. 等腰梯形 D. 矩形
相关试题

