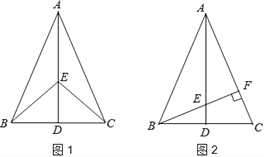
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由已知和等腰三角形的性质可得AB=AC,∠BAE=∠CAE,AE=AE,即可得到△ABE≌△ACE,应用全等三角形的性质可得BE=CE;
(2)由已知证得AF=BF,由(1)得∠EAF=∠CBF,再有∠AFE=∠BFC=90°,即可证得△AEF≌△BCF.
试题解析:证明:(1)∵AB=AC,D是BC的中点,∴∠BAE=∠CAE.
在△ABE和△ACE中,∵AB=AC,∠BAE=∠CAE,AE=AE,
∴△ABE≌△ACE.∴BE=CE.(运用垂直平分线的性质说明也可)
(2)∵∠BAC=45°,BF⊥AF,∴△ABF为等腰直角三角形.∴AF=BF.由(1)知AD⊥BC,∴∠EAF=∠CBF.
在△AEF和△BCF中,AF=BF,∠AFE=∠BFC=90°,∠EAF=∠CBF,
∴△AEF≌△BCF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(2,﹣3)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】在“数学晚会”上,七年级的10个同学藏在10个大盾牌后面,男同学盾牌前面的结果是一
个正数,女同学盾牌前面的结果是一个负数,这10个盾牌如图所示,请你通过计算,求出盾牌后面男、女同学各有多少人.
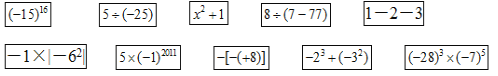
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A﹣C路径向终点C运动;点Q从B点出发沿B﹣C﹣A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为_________时,△PEC与△QFC全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,过B作BC⊥AB交⊙O于点C,过C作⊙O的切线交AB的延长线于点D,取AD的中点E,过E作EF∥BC交DC 的延长线与点F,连接AF并延长交BC的延长线于点G.
求证:(1)FC=FG (2)
 =BCCG.
=BCCG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个数的加上(或减去)这两个数的,这样的多项式叫做完全平方式;其特征是:
①多项式是项式;
②经升(降)幂排列后,首尾两项是且同号;中间项除符号外是首尾两项的积的2倍. -
科目: 来源: 题型:
查看答案和解析>>【题目】若平面直角坐标系内的点M在第四象限,且M到x轴的距离为1,到y轴的距离为2,则点M的坐标为( )
A.(2,1)
B.(﹣2,1)
C.(2,﹣1)
D.(1,﹣2)
相关试题

