【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.

(1)写出点C,D的坐标并求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由;
(3)如图2,点P是直线BD上的一个动点,连接PC,PO,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD,∠POB的数量关系.
参考答案:
【答案】(1)C(0,2),D(4,2).8;(2)F(1,0)或(5,0);(3)当点P在线段BD上运动时:∠OPC=∠PCD+∠POB;当点P在BD延长线上运动时:∠OPC=∠POB-∠PCD;当点P在DB延长线上运动时:∠OPC=∠PCD-∠POB.
【解析】试题分析:(1)根据点平移的规律易得点C的坐标为(0,2),点D的坐标为(4,2);四边形ABDC的面积=2×(3+1)=8;
(2)存在.设点P到AB的距离为h,则S△PAB=![]() ×AB×h,根据S△PAB=S四边形ABDC,列方程求h的值,确定P点坐标.
×AB×h,根据S△PAB=S四边形ABDC,列方程求h的值,确定P点坐标.
(3)分类讨论:当点P在线段BD上,作PM∥AB,根据平行线的性质由MP∥AB得∠2=∠POB,由CD∥AB得到CD∥MF,则∠1=∠PCD,所以∠OPC=∠POB+∠PCD;同样得到当点P在线段DB的延长线上,∠OPC=∠PCD-∠POB;当点P在线段BD的延长线上,得到∠OPC=∠POB-∠PCD.
试题解析:(1)依题意,得C(0,2),D(4,2),
∴S四边形ABDC=AB×OC=4×2=8;
(2)在y轴上是否存在一点P,使S△PAB=S四边形ABDC.理由如下:
设点P到AB的距离为h,
S△PAB=![]() ×AB×h=2h,
×AB×h=2h,
由S△PAB=S四边形ABDC,得2h=8,
解得h=4,
∴P(0,4)或(0,-4).
(3)当点P在线段BD上,作PM∥AB,如图1,
∵MP∥AB,
∴∠2=∠POB,
∵CD∥AB,
∴CD∥MP,
∴∠1=∠PCD,
∴∠OPC=∠1+∠2=∠POB+∠PCD;
当点P在线段DB的延长线上,作PN∥AB,如图2,
∵PN∥AB,
∴∠NPO=∠POB,
∵CD∥AB,
∴CD∥PN,
∴∠NPC=∠FCD,
∴∠OPC=∠NPC-∠NPO=∠FCD-∠POB;
同样得到当点P在线段BD的延长线上,得到∠OPC=∠POB-∠PCD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果“盈利5%”记作+5%,那么﹣3%表示( )
A. 盈利3% B. 亏损8% C. 盈利2% D. 亏损3%
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖随机抽样调查本班20名女同学所穿运动鞋尺码,并统计如表:
尺码/cm
21.5
22.0
22.5
23.0
23.5
人数
2
4
3
8
3
学校附近的商店经理根据表中决定本月多进尺码为23.0cm的女式运动鞋,商店经理的这一决定应用了哪个统计知识( )
A.众数
B.中位数
C.平均数
D.方差 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
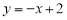 与反比例函数
与反比例函数 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.(1)求该反比例函数的表达式;
(2)若P为y轴上的点,且△AOP的面积是△AOB的面积的
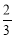 ,请求出点P的坐标.
,请求出点P的坐标.(3)写出直线
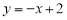 向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标。
向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标。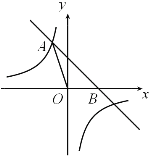
-
科目: 来源: 题型:
查看答案和解析>>【题目】“如果a>0,b<0,那么ab<0”的逆命题是_______________________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2=3x
(2)2x2﹣x﹣6=0.
相关试题

