【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图,点D在线段BC的延长线上移动,若∠BAC=40![]() ,则∠DCE=
,则∠DCE= ![]() .
.
(2)设∠BAC=m,∠DCE=n.
①如图,当点D在线段BC的延长线上移动时,m与n之间有什么数量关系?请说明理由.
②当点D在直线BC上(不与B、C重合)移动时,m与n之间有什么数量关系?请直接写出你的结论.

参考答案:
【答案】(1)40;(2)①m=n,理由见解析;②m+n=180°
【解析】试题分析:(1)可证△ABD≌△ACE,可得∠ACE=∠B,即可解题;
(2)①根据△ABD≌△ACE可分别求得∠BCE用m和用n分别表示,即可求得m、n的关系;②分两种情况分析,第1种,当D在线段BC的延长线上或反向延长线上时,第2种,当D在线段BC上时.
试题解析:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
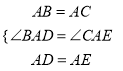 ,
,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠B,
∵AB=AC,∠BAC=40°,
∴∠ACE=∠B=70°,
∴∠DCE=180°70°70°=40°;
(2) ①∵△ABD≌△ACE(1)已证,
∴∠ACE=∠B,
∵AB=AC,∠BAC=m,
∴∠ACE=∠B=∠ACB=![]() ,
,
∴∠BCE=∠ACB+∠ACE=180°m,
∵∠BCE=180°∠DCE=180°n,
∴m=n.
②当D在线段BC的延长线上或反向延长线上时,m=n,
当D在线段BC上时,m+n=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=
 图象的两个交点.
图象的两个交点.(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣
 >0的解集.
>0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为正数,满足如下两个条件:a+b+c=32 ①
 ② 是否存在以
② 是否存在以  为三边长的三角形?如果存在,求出三角形的最大内角.
为三边长的三角形?如果存在,求出三角形的最大内角. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:ΔABE≌ΔACD,AB=10cm,∠A=60°,∠B=30°,则AD=_____ cm,∠ADC=_____。

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x2+x3=x5
B.2x2﹣x2=1
C.x2x3=x6
D.x6÷x3=x3 -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:ab2﹣a= .
相关试题

