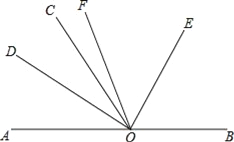
【题目】如图,点O为直线AB上一点,过点O作直线OC,已知∠AOC≠90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.求:
(1)当0°<∠AOC<90°时,求∠FOB+∠DOC的度数;
(2)若∠DOC=3∠COF,求∠AOC的度数.
参考答案:
【答案】(1)135°(2)∠AOC=67.5°或135°
【解析】(1)先根据射线OD平分∠AOC,∠AOD=∠COD,射线OE平分∠BOC,得∠COE=∠BOE,再根据∠AOC+∠BOC=180°,得出∠DOE=90°,由射线OF平分∠DOE,得∠DOF=∠EOF=45°,从而求得∠FOB+∠DOC的度数;
(2)设∠AOD=∠COD=x°,分∠AOC为锐角和钝角两种情况,根据∠DOC=3∠COF,得出x的值,即可求得∠AOC的度数.
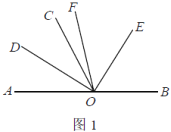
解:如图1,
(1)∵射线OD平分∠AOC,
∴∠AOD=∠COD,
∵射线OE平分∠BOC,
∴∠COE=∠BOE,
∵∠AOC+∠BOC=180°,
∴∠DOE=∠DOC+∠EOC=![]() ∠AOC+
∠AOC+![]() ∠BOC=90°,
∠BOC=90°,
∵OF平分∠DOE,
∴∠DOF=∠EOF=![]() ∠DOE=45°,
∠DOE=45°,
∴∠FOB+∠DOC=∠BOF+∠AOD=180°-∠DOF=280°-45°=135°;
(2)设∠AOD=∠COD=x°,则∠AOC=2x°,
由(1)的证明过程可知∠DOE=90°,∠DOF=∠EOF=45°,
∠AOC≠90°,分情况考虑如下:
①当∠AOC为锐角时,如图1,∠COF=∠DOF-∠COD=45°-x,
∵∠DOC=3∠COF,
∴x=3(45°-x),
解得x=33.75°,
∴∠AOC=2x=67.5°.
②当∠AOC为钝角时,如图2,
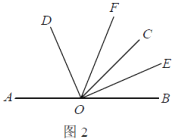
∠COF=∠COD-∠DOF=x-45°,
∵∠DOC=3∠COF,
∴x=3(x-45°),
解得x=67.5°,
∴∠AOC=2x=135°.
综合,可得∠AOC=67.5°或135°.
“点睛”本题考查了角的计算和角平分线的定义,一定要注意角平分线的几种表示方法.如:∠1=∠2,∠1=![]() ∠AOB,∠AOB=2∠1.
∠AOB,∠AOB=2∠1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.

(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
-
科目: 来源: 题型:
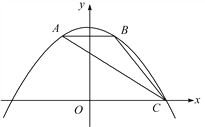
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,
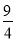 ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.
(1)如图①,若∠COF=34°,则∠BOE=________;若∠COF=m°,则∠BOE=________,∠BOE与∠COF的数量关系式为________;
(2)当射线OE绕点O逆时针旋转到如图②的位置时,(1)中∠BOE与∠COF的数量关系是否成立?请说明理由.
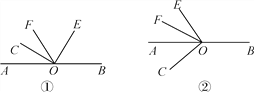
-
科目: 来源: 题型:
查看答案和解析>>【题目】点M(2,-3)关于原点对称的点N的坐标是: ( )
A. (-2,-3) B. (-2, 3) C. (2, 3) D. (-3, 2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在0,2,(﹣3)0,﹣5这四个数中,最大的数是( )
A. 0 B. 2 C. (﹣3)0 D. ﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A. y=﹣(x﹣1)2﹣3 B. y=﹣(x+1)2﹣3 C. y=﹣(x﹣1)2+3 D. y=﹣(x+1)2+3
相关试题

