【题目】甲乙两人同时登山,甲乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是 米/分钟,乙在A地提速时距地面的高度b为 米.
(2)若乙提速后,乙的速度是甲登山速度的3倍,请求出乙提速后y和x之间的函数关系式.
(3)登山多长时间时,乙追上了甲,此时乙距A地的高度为多少米?

参考答案:
【答案】(1)10,30;(2)y=30x﹣30;(3)登山6.5分钟,乙追上了甲,此时乙距A地的高度为135米.
【解析】
根据函数图象由甲走的路程除以时间就可以求出甲的速度;根据函数图象可以求出乙在提速前每分离开地面的高度是15米,就可以求出b的值;
(2)先根据乙的速度求出乙登上山顶的时间,求出B点的坐标,由待定系数法就可以求出解析式;
(3)由(2)的解析式建立方程求出其解就可以求出追上的时间,就可以求出乙离地面的高度,再减去A地的高度就可以得出结论.
解:(1)10,30
(2)设乙提速后的函数关系式为:y=kx+b,
由于乙提速后是甲的3倍,所以k=30,且图象经过(2.30)
所以30=2×30+b
解得:b=﹣30
所以乙提速后的关系式:y=30x﹣30.
(3)甲的关系式:设甲的函数关系式为:y=mx+n,
将n=100和点(20,300)代入,
求得 y=10x+100;
由题意得:10x+100=30x﹣30
解得:x=6.5 ,
把x=6.5代入y=10x+100=165,
相遇时乙距A地的高度为:165﹣30=135(米)
答:登山6.5分钟,乙追上了甲,此时乙距A地的高度为135米.
-
科目: 来源: 题型:
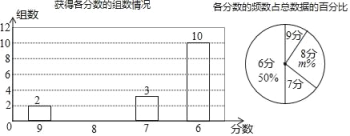
查看答案和解析>>【题目】目前由重庆市教育委员会,渝北区人们政府主办的“阳光下成长”重庆市第八届中小学生艺术展演活动落下帷幕,重庆一中学生舞蹈团、管乐团、民乐团、声乐团、话剧团等五大艺术团均荣获艺术表演类节目一等奖,重庆一中获优秀组织奖,重庆一中老师李珊获先进个人奖,其中重庆一中舞蹈团将代表重庆市参加明年的全国集中展演比赛,若以下两个统计图统计了舞蹈组各代表队的得分情况:
(1)m= ,在扇形统计图中分数为7的圆心角度数为 度.
(2)补全条形统计图,各组得分的中位数是 分,众数是 分.
(3)若舞蹈组获得一等奖的队伍有2组,已知主办方各组的奖项个数是按相同比例设置的,若参加该展演活动的总队伍数共有120组,那么该展演活动共产生了多少个一等奖?
-
科目: 来源: 题型:
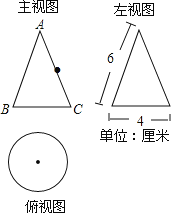
查看答案和解析>>【题目】如图是一个几何体的三视图.
(1)写出该几何体的名称,并根据所示数据计算这个几何体的表面积;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边的中点,分别过点B、C作射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)若AF=FD,在不添加辅助线的条件下,直接写出与△ABD面积相等的所有三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AC、BD交于点O,AD=15,AO=12.动点P以每秒2个单位的速度从点A出发,沿AC向点C匀速运动.同时,动点Q以每秒1个单位的速度从点D出发,沿DB向点B匀速运动.当其中有一点列达终点时,另一点也停止运动,设运动的时间为t秒.
(1)求线段DO的长;
(2)设运动过程中△POQ两直角边的和为y,请求出y关于x的函数解析式;
(3)请直接写出点P在线段OC上,点Q在线段DO上运动时,△POQ面积的最大值,并写出此时的t值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, ⊙O 的半径是2,直线l与⊙O 相交于A、B 两点,M、N 是⊙O 上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB 面积的最大值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2
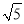 ,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.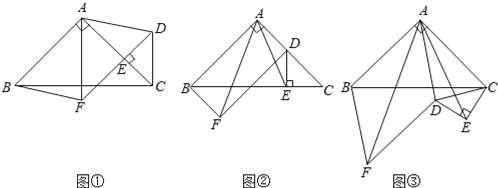
相关试题

