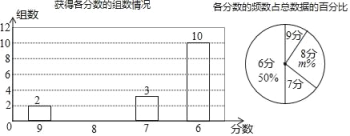
【题目】目前由重庆市教育委员会,渝北区人们政府主办的“阳光下成长”重庆市第八届中小学生艺术展演活动落下帷幕,重庆一中学生舞蹈团、管乐团、民乐团、声乐团、话剧团等五大艺术团均荣获艺术表演类节目一等奖,重庆一中获优秀组织奖,重庆一中老师李珊获先进个人奖,其中重庆一中舞蹈团将代表重庆市参加明年的全国集中展演比赛,若以下两个统计图统计了舞蹈组各代表队的得分情况:
(1)m= ,在扇形统计图中分数为7的圆心角度数为 度.
(2)补全条形统计图,各组得分的中位数是 分,众数是 分.
(3)若舞蹈组获得一等奖的队伍有2组,已知主办方各组的奖项个数是按相同比例设置的,若参加该展演活动的总队伍数共有120组,那么该展演活动共产生了多少个一等奖?
参考答案:
【答案】(1)25,54;(2)如图所示见解析;6.5,6;(3)该展演活动共产生了12个一等奖.
【解析】
(1)根据条形统计图和扇形统计图中的数据,即可得到总的组数,进而得出各分数对应的组数以及圆心角度数;(2)根据中位数以及众数的定义进行判断,即可得到中位数以及众数的值;(3)依据舞蹈组获得一等奖的队伍的比例,即可估计该展演活动共产生一等奖的组数.
(1)10÷50%=20(组),20﹣2﹣3﹣10=5(组),
m%=![]() ×100%=25%,
×100%=25%,
![]() ×360°=54°,
×360°=54°,
故答案为:25,54;
(2)8分这一组的组数为5,如图所示:
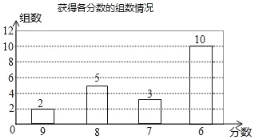
各组得分的中位数是![]() (7+6)=6.5,
(7+6)=6.5,
分数为6分的组数最多,故众数为6;
故答案为:6.5,6;
(3)由题可得,![]() ×120=12(组),
×120=12(组),
∴该展演活动共产生了12个一等奖.
-
科目: 来源: 题型:
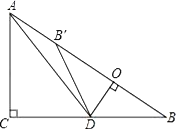
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).

(1)作出与△ABC关于x轴对称的△A1B1C1, 并写出A1、B1、C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2, 使
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
-
科目: 来源: 题型:
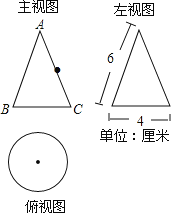
查看答案和解析>>【题目】如图是一个几何体的三视图.
(1)写出该几何体的名称,并根据所示数据计算这个几何体的表面积;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边的中点,分别过点B、C作射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)若AF=FD,在不添加辅助线的条件下,直接写出与△ABD面积相等的所有三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人同时登山,甲乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是 米/分钟,乙在A地提速时距地面的高度b为 米.
(2)若乙提速后,乙的速度是甲登山速度的3倍,请求出乙提速后y和x之间的函数关系式.
(3)登山多长时间时,乙追上了甲,此时乙距A地的高度为多少米?

相关试题

