【题目】如图,在菱形ABCD中,AC、BD交于点O,AD=15,AO=12.动点P以每秒2个单位的速度从点A出发,沿AC向点C匀速运动.同时,动点Q以每秒1个单位的速度从点D出发,沿DB向点B匀速运动.当其中有一点列达终点时,另一点也停止运动,设运动的时间为t秒.
(1)求线段DO的长;
(2)设运动过程中△POQ两直角边的和为y,请求出y关于x的函数解析式;
(3)请直接写出点P在线段OC上,点Q在线段DO上运动时,△POQ面积的最大值,并写出此时的t值.

参考答案:
【答案】(1)9(2)见解析(3)当t=![]() 时,△POQ面积的最大值
时,△POQ面积的最大值
【解析】
(1)根据菱形的对角线互相垂直平分的性质得到直角△AOD,在该直角三角形中利用勾股定理来求线段DO的长度;
(2)需要分类讨论:点P在线段OA上、点Q在线段OD上;点P在线段OC上,点Q在线段OD上;点P在线段OC上,点Q在线段OB上;
(3)由6<t≤9时OP=12﹣2t、OQ=9﹣t可得△POQ的面积S=![]() (9﹣t)(12﹣2t)=﹣t2+15t﹣54=﹣(t﹣
(9﹣t)(12﹣2t)=﹣t2+15t﹣54=﹣(t﹣![]() )2+
)2+![]() ,利用二次函数的性质求解可得.
,利用二次函数的性质求解可得.
(1)∵四边形ABCD是菱形,
∴AC⊥BD.
在Rt△AOD中,AD=15,AO=12
由勾股定理得:
OD=![]() =9.
=9.
(2)①当0≤t≤6时,OP=12﹣2t,OQ=9﹣t,则OP+OQ=12﹣2t+9﹣t=﹣3t+21
即:y=﹣3t+21;
②当6<t≤9时,OP=2t﹣12,OQ=9﹣t,则OP+OQ=2t﹣12+9﹣t=t﹣3
即:y=t﹣3;
③当9<t≤12时,OP=2t﹣12,OQ=t﹣9,则OP+OQ=2t﹣12+t﹣9=3t﹣21
即:y=3t﹣21;
综上所述:y=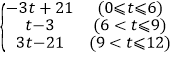 ;
;
(3)如图,
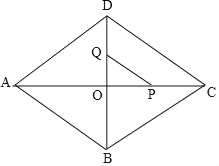
当6<t≤9时,∵OP=12﹣2t、OQ=9﹣t,
∴△POQ的面积S=![]() (9﹣t)(12﹣2t)
(9﹣t)(12﹣2t)
=﹣t2+15t﹣54
=﹣(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,△POQ面积的最大值.
时,△POQ面积的最大值.
-
科目: 来源: 题型:
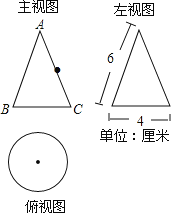
查看答案和解析>>【题目】如图是一个几何体的三视图.
(1)写出该几何体的名称,并根据所示数据计算这个几何体的表面积;
(2)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边的中点,分别过点B、C作射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)若AF=FD,在不添加辅助线的条件下,直接写出与△ABD面积相等的所有三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人同时登山,甲乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是 米/分钟,乙在A地提速时距地面的高度b为 米.
(2)若乙提速后,乙的速度是甲登山速度的3倍,请求出乙提速后y和x之间的函数关系式.
(3)登山多长时间时,乙追上了甲,此时乙距A地的高度为多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, ⊙O 的半径是2,直线l与⊙O 相交于A、B 两点,M、N 是⊙O 上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB 面积的最大值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2
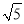 ,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.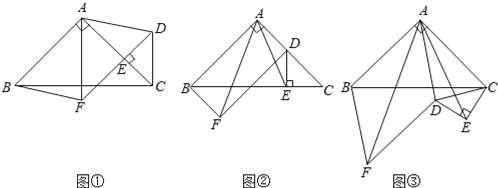
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-2,0),顶点坐标为(2,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①当x>6时,y<0;②5a+b>0;③
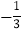 ≤a≤-
≤a≤-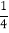 ,④4≤n<5中,正确有( )
,④4≤n<5中,正确有( )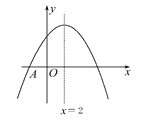
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

