【题目】已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1 , l2的表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,过点C,D分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.
①设点C的纵坐标为a,求点D的坐标(用含a的代数式表示)
②若矩形CDEF的面积为60,请直接写出此时点C的坐标.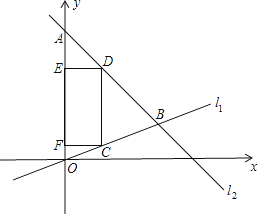
参考答案:
【答案】
(1)
解:设直线l1的表达式为y=k1x,它过(18,6)得18k1=6 k1= ![]()
∴y= ![]() x
x
设直线l2的表达式为y=k2x+b,它过点A(0,24),B(18,6)
得 ![]() 解得
解得 ![]() ,
,
∴直线l2的表达式为:y=﹣x+24;
(2)
解:①∵点C在直线l1上,且点C的纵坐标为a,
∴a= ![]() x x=3a,
x x=3a,
∴点C的坐标为(3a,a),
∵CD∥y轴
∴点D的横坐标为3a,
∵点D在直线l2上,
∴y=﹣3a+24
∴D(3a,﹣3a+24)
②∵C(3a,a),D(3a,﹣3a+24)
∴CF=3a,CD=﹣3a+24﹣a=﹣4a+24,
∵矩形CDEF的面积为60,
∴S矩形CDEF=CFCD=3a×(﹣4a+24)=60,解得a=1或a=5,
当a=1时,3a=3,故C(3,1);
当a=5时,3a=15,故C(15,5);
综上所述C点坐标为:C(3,1)或(15,5).
【解析】(1)设直线l1的表达式为y=k1x,它过(18,6)可求出k1的值,进而得出其解析式;设直线l2的表达式为
y=k2x+b,由于它过点A(0,24),B(18,6),故把此两点坐标代入即可求出k2 , b的值,进而得出其解析式;(2)①因为点C在直线l1上,且点C的纵坐标为a,故把y=a代入直线l1的表达式即可得出x的值,进而得出C点坐标,由于CD∥y轴,所以点D的横坐标为3a,再根据点D在直线l2上即可得出点D的纵坐标,进而得出结论;
②先根据CD两点的坐标用a表示出CF及CD的值,由矩形的面积为60即可求出a的值,进而得出C点坐标.
【考点精析】关于本题考查的一次函数的性质和一次函数的图象和性质,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.

(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师用
 个
个 的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边
的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边 共享,或有一面
共享,或有一面 共享.老师拿出一张
共享.老师拿出一张 的方格纸(如图②),请小荣将此
的方格纸(如图②),请小荣将此 个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有________种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有________种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市用3 000元购进某种干果销售,由于销售状况良好,超市又调拨9 000元购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量比第一次的2倍还多300 kg.如果超市按9元/kg的价格出售,当大部分干果售出后,余下的600 kg按售价的八折售完.
(1)该种干果第一次的进价是多少?
(2)超市销售这种干果共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】准备一张矩形纸片,按如图操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.

(1)、求证:四边形BFDE是平行四边形;
(2)、若四边形BFDE是菱形, AB=2,求菱形BFDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线y=﹣2x+4与两坐标轴分别交于点A、B,点C为线段OA上一动点,连接BC,作BC的中垂线分别交OB、AB交于点D、E.
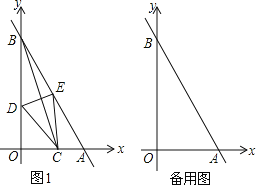
(l)当点C与点O重合时,DE= ;
(2)当CE∥OB时,证明此时四边形BDCE为菱形;
(3)在点C的运动过程中,直接写出OD的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

相关试题

