【题目】如图AB∥CD,EF分别交AB于点F,交CD于点E,EF与DB交于点G,且EA平分∠CEF,∠BFG=70°.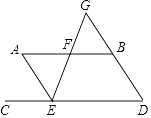
(1)求∠A的度数.
(2)若∠A=∠D,求证:∠AEF=∠G.
参考答案:
【答案】
(1)解:∵∠AFE=∠BFG=70°,
∵AB∥CD,
∴∠CEF=180°﹣∠AFE=110°,
∵且EA平分∠CEF,
∴∠AEF= ![]() CEF=55°,
CEF=55°,
∴∠A=180°﹣∠AFE﹣∠AEF=55°
(2)解:∵AB∥CD,
∴∠GED=∠GFB=70°,
∵∠D=∠A=55°,
∴∠G=55°,
∴∠AEF=∠G
【解析】(1)由AB∥CD可得同旁内角互补,即∠CEF=180°﹣∠AFE=110°,由EA平分∠CEF,∠A可转化为∠ AEC,即可求出;(2)由(1)∠AEF=∠A,可求出∠G=55°,即∠AEF=∠G.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠1=∠2=50°.
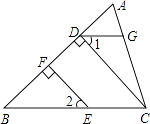
(1)求证:EF∥CD;
(2)若∠AGD=65°,试求∠DCG的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:解不等式(x+2)(x﹣3)>0,根据有理数的乘法法则“两数相乘,同号得正”,可以转化为不等式组求解.
解:(x+2)(x﹣3)>0,转化为①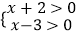 或②
或② 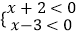 ,解不等式组①,得x>3,解不等式组②,得x<﹣2.
,解不等式组①,得x>3,解不等式组②,得x<﹣2.
∴原不等式(x+2)(x﹣3)>0的解集是x>3或x<﹣2.
请你仿照上面的方法,解下列不等式
(1)(x+7)(2x+8)>0
(2)(3x﹣9)(x+11)<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人分别在六次射击中的成绩如下表:(单位:环)
第1次
第2次
第3次
第4次
第5次
第6次
甲
6
7
7
8
6
8
乙
5
9
6
8
5
9
分别算出两人射击的平均数和方差.这六次射击中成绩发挥比较稳定的是谁?
-
科目: 来源: 题型:
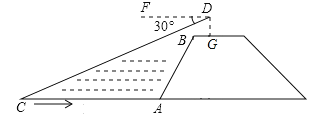
查看答案和解析>>【题目】如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小华的眼睛与地面的距离是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=8米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长为 米.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆锥的底面半径为1,母线长为2,则它的侧面积为_____.(结果保留π)
相关试题

