【题目】已知:如图,在等腰直角三角形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,且
的中点,且![]() ,垂足为点
,垂足为点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,联结
,联结![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
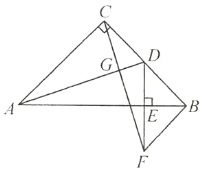
参考答案:
【答案】(1)见解析;(2)![]() 是等腰三角形,理由见解析.
是等腰三角形,理由见解析.
【解析】
(1)由![]() 和
和![]() 证明△DBF=等腰直角三角形,再证明
证明△DBF=等腰直角三角形,再证明![]() ,得
,得![]() ,从而证明
,从而证明![]() ;
;
(2)证明![]() ,可得
,可得![]() ,再由(1)知
,再由(1)知![]() ,从而证明
,从而证明![]() ,即可说明△ACF的性质.
,即可说明△ACF的性质.
(1)证明:![]() ,
,![]() ,
,
![]() ,
,
∵![]() ,
,
∴∠FEB=90°,
∴∠BFE=45°,
∴△DBF=等腰直角三角形,
∴DB=BF,
∵![]() 为
为![]() 的中点,
的中点,
∴DC=BD,
∴DC=FB,
在△ACD和△CBF中
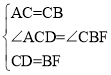
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
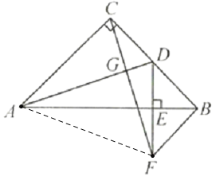
(2)连接![]() ,
,
由(1)知△DBF等腰直角三角形,
![]() ,
,
∴DE=FE,
在△ADE和△AFE中
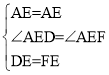
![]() ,
,
![]() ,
,
由(1)知![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰三角形.
是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂线,交BC于P点,则P即为所求;
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求.
对于两人的作法,下列判断何者正确?( )

A. 两人皆正确B. 两人皆错误C. 甲正确,乙错误D. 甲错误,乙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在
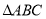 中,
中,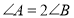 ,
,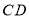 平分
平分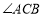 ,
,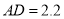 ,
,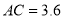 ,求
,求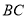 的长.
的长.小聪思考:因为
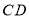 平分
平分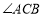 ,所以可在
,所以可在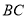 边上取点
边上取点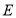 ,使
,使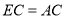 ,连接
,连接 .这样很容易得到
.这样很容易得到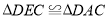 ,经过推理能使问题得到解决(如图2).
,经过推理能使问题得到解决(如图2).请回答:(1)
 是 三角形.
是 三角形.(2)
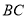 的长为 .
的长为 .参考小聪思考问题的方法,解决问题:
(3)如图3,已知
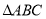 中,
中,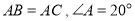 ,
, 平分
平分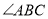 ,
,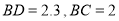 .求
.求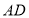 的长.
的长.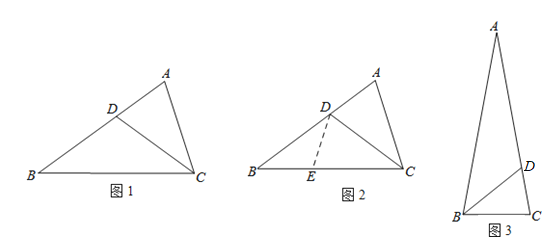
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列命题中,写出其逆命题,并判断逆命题的真假.
(1)如果两个角相等,那么它们都是对顶角;
(2)直角都相等;
(3)两条平行线被第三条直线所截,所成的同位角相等;
(4)如果
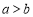 ,那么
,那么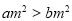 ;
;(5)如果一个三角形是直角三角形,那么它的两个锐角互余.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB经过x轴上的点A(2,0),且与抛物线相交于B、C两点,已知B点坐标为(1,1) .
(1)求直线和抛物线的解析式;
(2)如果D为抛物线上一点,使得△AOD与△OBC的面积相等,求D点坐标。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是( )
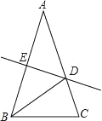
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 80° B. 90° C. 100° D. 130°
相关试题

