【题目】如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F. 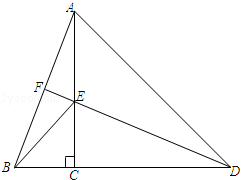
(1)求证:DE⊥AB;
(2)若已知BC=a,AC=b,AB=c,设EF=x,则△ABD的面积用代数式可表示为;S△ABD= ![]() c(c+x)你能借助本题提供的图形,证明勾股定理吗?试一试吧.
c(c+x)你能借助本题提供的图形,证明勾股定理吗?试一试吧.
参考答案:
【答案】
(1)证明:在Rt△ABC和Rt△DCE中,
![]()
∴Rt△ABC≌Rt△DCE(HL)
∴∠BAC=∠EDC(全等三角形的对应角相等),
∵∠AEF=∠DEC(对顶角相等),∠EDC+∠DEC=90°(直角三角形两锐角互余),
∴∠BAC+∠AEF=∠EDC+∠DEC=90°.
∴∠AFE=180°﹣(∠BAC+∠AEF)=90°.
∴DE⊥AB
(2)解:由题意知:
S△ABD=S△BCE+S△ACD+S△ABE= ![]() a2+
a2+ ![]() b2+
b2+ ![]() cx,
cx,
∵ ![]() ,
,
∴ ![]() .
.
∴a2+b2=c2
【解析】(1)首先证明Rt△ABC≌Rt△DCE,得出∠BAC=∠EDC,进而求出∠AFE=180°﹣(∠BAC+∠AEF)=90°,即可得出答案;(2)根据S△ABD=S△BCE+S△ACD+S△ABE , ![]() 得出a2+b2=c2即可.
得出a2+b2=c2即可.
-
科目: 来源: 题型:
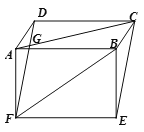
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
(1) 试说明DF=CE;
(2) 若AC=BF=DF,求∠ACE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数:3,0,﹣10,0.58,﹣(﹣6),﹣|﹣9|,(﹣4)2 中,负数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元)与他买这种笔记本的本数x之间的关系是( )
A. Q=8x B. Q=8x﹣50 C. Q=50﹣8x D. Q=8x+50
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28,∠AGF=80,FH平分∠EFG.

(1)说明:DC∥AB;
(2)求∠PFH的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:
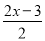 -
-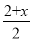 =-1; (2)解不等式组:
=-1; (2)解不等式组: 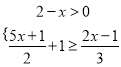
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.

(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
相关试题

