【题目】在![]() 中,射线
中,射线![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 边上运动(不与点
边上运动(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
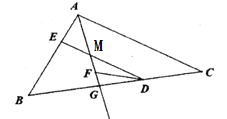
(1)如图1,点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 平分
平分![]() .
.


①若![]() ,
,![]() ,则
,则![]() _____;若
_____;若![]() ,则
,则![]() _____;
_____;
②试探究![]() 与
与![]() 之间的数量关系?请说明理由;
之间的数量关系?请说明理由;
(2)点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 的角平分线所在直线与射线
的角平分线所在直线与射线![]() 交于点
交于点![]() .试探究
.试探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
参考答案:
【答案】(1)①115°,110°;②![]() ,证明见解析;(2)
,证明见解析;(2)![]() ,证明见解析.
,证明见解析.
【解析】
(1)①根据角平分线的定义求得∠CAG=![]() ∠BAC=50°;再由平行线的性质可得∠EDG=∠C=30°,∠FMD=∠GAC=50°;由三角形的内角和定理求得∠AFD的度数即可;已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=
∠BAC=50°;再由平行线的性质可得∠EDG=∠C=30°,∠FMD=∠GAC=50°;由三角形的内角和定理求得∠AFD的度数即可;已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=![]() ∠BAC,∠FDM=
∠BAC,∠FDM=![]() ∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;即可得∠FDM +∠FMD=
∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;即可得∠FDM +∠FMD=![]() ∠EDG +∠GAC=
∠EDG +∠GAC=![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×140°=70°;再由三角形的内角和定理可求得∠AFD=110°;②∠AFD=90°+
×140°=70°;再由三角形的内角和定理可求得∠AFD=110°;②∠AFD=90°+![]() ∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=
∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=![]() ∠BAC,∠FDM=
∠BAC,∠FDM=![]() ∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;由此可得∠FDM +∠FMD=
∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;由此可得∠FDM +∠FMD=![]() ∠EDG +∠GAC=
∠EDG +∠GAC=![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×(180°-∠B)=90°-
×(180°-∠B)=90°-![]() ∠B;再由三角形的内角和定理可得∠AFD=90°+
∠B;再由三角形的内角和定理可得∠AFD=90°+![]() ∠B;(2)∠AFD=90°-
∠B;(2)∠AFD=90°-![]() ∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=
∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=![]() ∠BAC,∠NDE=
∠BAC,∠NDE=![]() ∠EDB,即可得∠FDM=∠NDE=
∠EDB,即可得∠FDM=∠NDE=![]() ∠EDB;由DE//AC,根据平行线的性质可得∠EDB=∠C,∠FMD=∠GAC;即可得到∠FDM=∠NDE=
∠EDB;由DE//AC,根据平行线的性质可得∠EDB=∠C,∠FMD=∠GAC;即可得到∠FDM=∠NDE=![]() ∠C,所以∠FDM +∠FMD =
∠C,所以∠FDM +∠FMD =![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×(180°-∠B)=90°-
×(180°-∠B)=90°-![]() ∠B;再由三角形外角的性质可得∠AFD=∠FDM +∠FMD=90°-
∠B;再由三角形外角的性质可得∠AFD=∠FDM +∠FMD=90°-![]() ∠B.
∠B.
(1)①∵AG平分∠BAC,∠BAC=100°,
∴∠CAG=![]() ∠BAC=50°;
∠BAC=50°;
∵![]() ,∠C=30°,
,∠C=30°,
∴∠EDG=∠C=30°,∠FMD=∠GAC=50°;
∵DF平分∠EDB,
∴∠FDM=![]() ∠EDG=15°;
∠EDG=15°;
∴∠AFD=180°-∠FMD-∠FDM=180°-50°-15°=115°;
∵∠B=40°,
∴∠BAC+∠C=180°-∠B=140°;
∵AG平分∠BAC,DF平分∠EDB,
∴∠CAG=![]() ∠BAC,∠FDM=
∠BAC,∠FDM=![]() ∠EDG,
∠EDG,
∵DE//AC,
∴∠EDG=∠C,∠FMD=∠GAC;
∴∠FDM +∠FMD=![]() ∠EDG +∠GAC=
∠EDG +∠GAC=![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×140°=70°;
×140°=70°;
∴∠AFD=180°-(∠FDM +∠FMD)=180°-70°=110°;
故答案为:115°,110°;
②∠AFD=90°+![]() ∠B,理由如下:
∠B,理由如下:
∵AG平分∠BAC,DF平分∠EDB,
∴∠CAG=![]() ∠BAC,∠FDM=
∠BAC,∠FDM=![]() ∠EDG,
∠EDG,
∵DE//AC,
∴∠EDG=∠C,∠FMD=∠GAC;
∴∠FDM +∠FMD=![]() ∠EDG +∠GAC=
∠EDG +∠GAC=![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×(180°-∠B)=90°-
×(180°-∠B)=90°-![]() ∠B;
∠B;
∴∠AFD=180°-(∠FDM +∠FMD)=180°-(90°-![]() ∠B)=90°+
∠B)=90°+![]() ∠B;
∠B;
(2)∠AFD=90°-![]() ∠B,理由如下:
∠B,理由如下:
如图,射线ED交AG于点M,
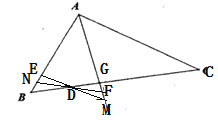
∵AG平分∠BAC,DF平分∠EDB,
∴∠CAG=![]() ∠BAC,∠NDE=
∠BAC,∠NDE=![]() ∠EDB,
∠EDB,
∴∠FDM=∠NDE=![]() ∠EDB,
∠EDB,
∵DE//AC,
∴∠EDB=∠C,∠FMD=∠GAC;
∴∠FDM=∠NDE=![]() ∠C,
∠C,
∴∠FDM +∠FMD =![]() ∠C+
∠C+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ×(180°-∠B)=90°-
×(180°-∠B)=90°-![]() ∠B;
∠B;
∴∠AFD=∠FDM +∠FMD=90°-![]() ∠B.
∠B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 与直线
与直线 和
和 分别交于点
分别交于点 、
、 ,且
,且 ,
, 、
、 分别是
分别是 和
和 上两点,连接
上两点,连接 ,
, .
.
(1)试说明:
 ;
;(2)如果
 ,
, ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形
 中,
中,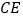 平分
平分 交
交 于点
于点 ,点
,点 在线段
在线段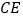 上运动.
上运动.(1)如图1,已知
 .
.
①若
 平分
平分 ,则
,则 ______;
______;②若
 ,试说明
,试说明 ;
;(2)如图2,已知
 ,试说明
,试说明 平分
平分 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,回答问题:
若整数
 能被4整除,则称整数
能被4整除,则称整数 为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。
为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。(1)10到15之间的“完美数”是_______;
若
 ,
, 是整数,则
是整数,则 ________ “完美数”(填:“是”或“不是”);
________ “完美数”(填:“是”或“不是”);(2)若任意四个连续的“完美数”中最小数的是4
 (
( 是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;
是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;(3)当
 是正整数时,试说明:
是正整数时,试说明: 一定是“完美数”.
一定是“完美数”. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
①在同一平面内不相交的两条线段必平行
②过两条直线
 外一点
外一点 ,一定可做直线
,一定可做直线 ,使
,使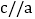 ,且
,且
③过直线外一点有且只有一条直线与已知直线平行
④两直线被第三条直线所截得的同旁内角的平分线互相垂直
A. 0个B. 1个C. 2个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B是反比例函数y=
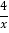 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是_____.
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,点
,点 是
是 上一个动点,连接
上一个动点,连接 ,将
,将 沿
沿 折叠,点
折叠,点 落在点
落在点 处,连接
处,连接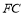 ,若
,若 是直角三角形,则
是直角三角形,则 的长为___________.
的长为___________.
相关试题

