【题目】在四边形![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上运动.
上运动.
(1)如图1,已知![]() .
.

①若![]() 平分
平分![]() ,则
,则![]() ______;
______;
②若![]() ,试说明
,试说明![]() ;
;
(2)如图2,已知![]() ,试说明
,试说明![]() 平分
平分![]() .
.

参考答案:
【答案】(1)①90°;②证明见解析;(2)证明见解析.
【解析】
(1)①由![]() 可得
可得![]() ,根据平行线的性质可得∠ABC+∠BCD=180°,已知BF平分∠ABC,CE平分∠BCD,由角平分线的定义可得∠FBC=
,根据平行线的性质可得∠ABC+∠BCD=180°,已知BF平分∠ABC,CE平分∠BCD,由角平分线的定义可得∠FBC=![]() ∠ABC,∠BCF=
∠ABC,∠BCF=![]() ∠BCD,所以∠FBC+∠BCF=
∠BCD,所以∠FBC+∠BCF=![]() ∠ABC+
∠ABC+![]() ∠BCD=
∠BCD=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×180°=90°,即可得∠BFC=90°;②已知CE平分∠BCD,由角平分线的定义可得∠DCE=∠BCF,根据等角的余角相等可得∠FBC=∠DEC;再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得
×180°=90°,即可得∠BFC=90°;②已知CE平分∠BCD,由角平分线的定义可得∠DCE=∠BCF,根据等角的余角相等可得∠FBC=∠DEC;再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得![]() ;(2)已知CE平分∠BCD,由角平分线的性质可得∠DCE=∠BCF,由三角形的内角和定理可证得∠FBC=∠DEC;由∠BFC+∠BFE=180°,∠BFC=∠A,可得∠BFE+∠A=180°,再由四边形的内角和为360°可得∠ABF+∠AEF=180°,再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得
;(2)已知CE平分∠BCD,由角平分线的性质可得∠DCE=∠BCF,由三角形的内角和定理可证得∠FBC=∠DEC;由∠BFC+∠BFE=180°,∠BFC=∠A,可得∠BFE+∠A=180°,再由四边形的内角和为360°可得∠ABF+∠AEF=180°,再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得![]() .
.
(1)∵![]() ,
,
∴![]() ,
,
∴∠ABC+∠BCD=180°,
∵BF平分∠ABC,CE平分∠BCD,
∴∠FBC=![]() ∠ABC,∠BCF=
∠ABC,∠BCF=![]() ∠BCD,
∠BCD,
∴∠FBC+∠BCF=![]() ∠ABC+
∠ABC+![]() ∠BCD=
∠BCD=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×180°=90°,
×180°=90°,
∴∠BFC=90°;
故答案为:90°;
②∵CE平分∠BCD,
∴∠DCE=∠BCF,
∵∠BFC=∠D=90°,
∴∠BCF+∠FBC=90°,∠DEC+∠ECD=90°,
∴∠FBC=∠DEC;
∵∠ABF+∠AEF=180°,∠DEC+∠AEF=180°,
∴∠ABF=∠DEC,
∴∠DEC=∠ABF=∠FBC,
∴![]() ;
;
(2)∵CE平分∠BCD,
∴∠DCE=∠BCF,
∵∠BFC=∠D,
∴∠FBC=∠DEC;
∵∠BFC+∠BFE=180°,∠BFC=∠A,
∴∠BFE+∠A=180°,
∴∠ABF+∠AEF=180°,
∵∠DEC+∠AEF=180°,
∴∠ABF=∠DEC,
∴∠DEC=∠ABF=∠FBC,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 ,把
,把 的直角三角板
的直角三角板 的直角顶点
的直角顶点 放在直线
放在直线 上.将直角三角板
上.将直角三角板 在平面内绕点
在平面内绕点 任意转动,若转动的过程中,直线
任意转动,若转动的过程中,直线 与直线
与直线 的夹角为60°,则
的夹角为60°,则 的度数为___.
的度数为___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A.
 B. 2 C.
B. 2 C.  D. 2
D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 与直线
与直线 和
和 分别交于点
分别交于点 、
、 ,且
,且 ,
, 、
、 分别是
分别是 和
和 上两点,连接
上两点,连接 ,
, .
.
(1)试说明:
 ;
;(2)如果
 ,
, ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,回答问题:
若整数
 能被4整除,则称整数
能被4整除,则称整数 为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。
为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。(1)10到15之间的“完美数”是_______;
若
 ,
, 是整数,则
是整数,则 ________ “完美数”(填:“是”或“不是”);
________ “完美数”(填:“是”或“不是”);(2)若任意四个连续的“完美数”中最小数的是4
 (
( 是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;
是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;(3)当
 是正整数时,试说明:
是正整数时,试说明: 一定是“完美数”.
一定是“完美数”. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
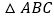 中,射线
中,射线 平分
平分 交
交 于点
于点 ,点
,点 在
在 边上运动(不与点
边上运动(不与点 重合),过点
重合),过点 作
作 交
交 于点
于点 .
.(1)如图1,点
 在线段
在线段 上运动时,
上运动时, 平分
平分 .
.

①若
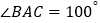 ,
, ,则
,则 _____;若
_____;若 ,则
,则 _____;
_____;②试探究
 与
与 之间的数量关系?请说明理由;
之间的数量关系?请说明理由;(2)点
 在线段
在线段 上运动时,
上运动时, 的角平分线所在直线与射线
的角平分线所在直线与射线 交于点
交于点 .试探究
.试探究 与
与 之间的数量关系,并说明理由.
之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
①在同一平面内不相交的两条线段必平行
②过两条直线
 外一点
外一点 ,一定可做直线
,一定可做直线 ,使
,使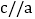 ,且
,且
③过直线外一点有且只有一条直线与已知直线平行
④两直线被第三条直线所截得的同旁内角的平分线互相垂直
A. 0个B. 1个C. 2个D. 3个
相关试题

