【题目】已知,如图1,抛物线![]() 过点
过点![]() 且对称轴为直线
且对称轴为直线![]() 点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
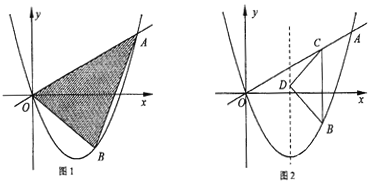
(1)求该抛物线的解析式:
(2)若△OAB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)如图2,过点B作直线BC∥y轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使△BCD是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;
;
(2)S![]() ,
, ![]() ;
;
(3)存在,点B为![]() 或
或![]()
【解析】试题分析:(1)根据抛物线![]() 过点
过点![]() 且对称轴为直线
且对称轴为直线![]() 即可求得结果;
即可求得结果;
(2)过点B作![]() 轴,交
轴,交![]() 于点
于点![]() ,则可得直线
,则可得直线![]() 为
为![]() ,则可设点
,则可设点![]() ,点
,点![]() 即可表示出BH,再根据三角形的面积公式即可表示出S关于m的函数关系式,根据二次函数的性质即可求得最大值;
即可表示出BH,再根据三角形的面积公式即可表示出S关于m的函数关系式,根据二次函数的性质即可求得最大值;
(3)设在抛物线的对称轴![]() 上存在点D满足题意,过点D作
上存在点D满足题意,过点D作![]() 于点Q,则由(2)有点
于点Q,则由(2)有点![]() ,点B
,点B![]() ,即可表示BC,由△BCD是以D为直角顶点的等腰直角三角形可得
,即可表示BC,由△BCD是以D为直角顶点的等腰直角三角形可得![]() ,则可得
,则可得![]() 且
且![]() ,再结合绝对值的性质分类讨论即可.
,再结合绝对值的性质分类讨论即可.
(1)由题知: 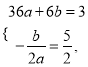 解之,得
解之,得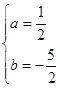
![]() 该抛物线的解析式为:
该抛物线的解析式为:![]()
(2)过点B作![]() 轴,交
轴,交![]() 于点
于点![]() 由题知直线
由题知直线![]() 为:
为:![]()
![]() 设点
设点![]() 点
点![]()
![]()
![]()
![]()
![]()
![]()
(3)设在抛物线的对称轴![]() 上存在点D满足题意,
上存在点D满足题意,
过点D作![]() 于点Q,则由(2)有点
于点Q,则由(2)有点![]() ,点B
,点B![]()
![]()
![]() 是以D为直角顶点的等腰直角三角形
是以D为直角顶点的等腰直角三角形
![]() 即是:
即是: ![]() 且
且![]()
若![]() 解之:
解之:![]() (舍去),
(舍去),![]()
![]() 时,
时, ![]()
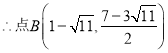
若![]() 解之:
解之:![]() (舍去)
(舍去)
当![]() 时,
时, ![]()
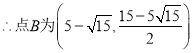
综上,满足条件的点B为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式(a-2)x>a-2可以变形为x<1,则a的取值范围为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学库存960套旧课桌椅准备修理。现有甲、乙两个木工小组都想承接这项业务。经协商后得知:甲小组单独修理这批桌椅比乙小组多用20天;乙小组每天比甲小组多修8套;学校每天需付甲小组修理费80元,付乙小组120元。
(1)求甲、乙两个小组每天各修理桌櫈多少套?
(2)在修理过程中,学校要委派一名修理工进行质量监督,并由学校负担他每天的生活补助10元,现有以下三种修理方案供选择:①由甲单独修理;②由乙单独修理;③由甲、乙共同合作修理。你认为哪种方案既省时又省钱?试比较说明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a|=8,|b|=3,当a、b异号时,求a﹣b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b互为相反数,c,d互为倒数,x的绝对值为2,求a+b+x2﹣cdx.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线y=x2﹣x﹣12与x轴分别交于A,B两点,则AB的长为
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A. 平行四边形的对角线相等
B. 对顶角相等
C. 两条腰对应相等的两个等腰三角形全等
D. 同旁内角相等,两直线平行
相关试题

