【题目】若抛物线y=x2﹣x﹣12与x轴分别交于A,B两点,则AB的长为
参考答案:
【答案】7
【解析】解:解方程x2﹣x﹣12=0得x1=4,x2=﹣3,则A(﹣3,0),B(4,0),
所以AB=4﹣(﹣3)=7.
所以答案是7.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a|=8,|b|=3,当a、b异号时,求a﹣b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图1,抛物线
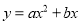 过点
过点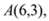 且对称轴为直线
且对称轴为直线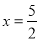 点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
点B为直线OA下方的抛物线上一动点,点B的横坐标为m.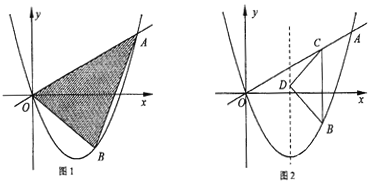
(1)求该抛物线的解析式:
(2)若△OAB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)如图2,过点B作直线BC∥y轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使△BCD是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b互为相反数,c,d互为倒数,x的绝对值为2,求a+b+x2﹣cdx.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A. 平行四边形的对角线相等
B. 对顶角相等
C. 两条腰对应相等的两个等腰三角形全等
D. 同旁内角相等,两直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四种说法:①顶点在圆心的角是圆心角;②两个圆心角相等,它们所对的弦也相等;③两条弧的长度相等,则这两条弧所对的圆心角相等;④在等圆中,圆心角不等,所对的弦也不等.其中正确的是______.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程2x2﹣5x+1=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
相关试题

