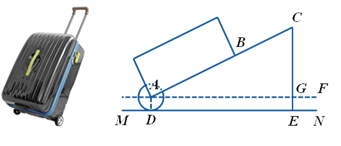
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆![]() 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,![]() =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:![]() ,
,![]() ,
,![]() )
)
参考答案:
【答案】(1) 8cm;(2) 30 cm.
【解析】分析:(1)作BH⊥AF于点G,交DM于点H,则△ABH∽△ACG,设圆形滚轮的半径AD的长是xcm,根据相似三角形的对应边的比相等,即可列方程求得x的值;
(2)根据BC=AC-AB进行计算即可.
详解:(1)作BK⊥MN于点K,交AF于点H,设⊙A的半径长x;
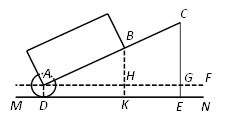
∵BK,CE都垂直于MN,
∴BK∥CE,
∴△ABH∽△ACG,
∴![]() ,即:
,即:![]() ,
,
解得:![]() ,
,
即⊙A的半径等于8cm;
(2)∵![]() cm,⊙A的半径等于8 cm,
cm,⊙A的半径等于8 cm,
∴![]() cm,
cm,
∵![]() ,
,
∴![]() cm,
cm,
∴![]() cm.
cm.
即:此时拉杆![]() 的伸长距离约为30 cm.
的伸长距离约为30 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】给出如下结论:①单项式
 的系数为
的系数为 ,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+
,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+ )﹣2(x
)﹣2(x )的结果是﹣x+
)的结果是﹣x+ ;④若单项式
;④若单项式 与
与 的差仍是单项式,则m+n=5.其中正确的结论有( )
的差仍是单项式,则m+n=5.其中正确的结论有( )A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(
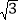 ,
,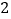 ),顶点C、D在x轴上,且OC=OD.
),顶点C、D在x轴上,且OC=OD.(1)当⊙P的半径为4时,
①在P1(
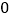 ,
,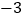 ),P2(
),P2(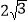 ,
,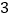 ),P3(
),P3(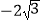 ,
,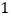 )中可以成为矩形ABCD的“等距圆”的圆心的是 ;
)中可以成为矩形ABCD的“等距圆”的圆心的是 ;②如果点P在直线
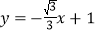 上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;(2)已知点P在
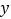 轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.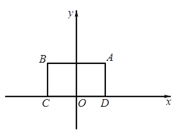
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b经过点A(5,0),B(1,4).

(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4≥kx+b的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有关部门从甲、乙两个城市所有的自动售货机中分别随机抽取了16台,记录下每一天各自的销售情况(单位:元):
甲:18,8,10,43,5,30,10,22,6,27,25,58,14,18,30,41.
乙:22,31,32,42,20,27,48,23,38,43,12,34,18,10,34,23.
小明用图1表示甲城市16台自动售货机的销售情况,小亮用图2表示甲城市16台自动售货机的销售情况.

(1)请你仔细观察图1,你能从中获得哪些信息?(写出两条不同信息)
(2)请你仔细观察图2,把图2的统计图补充完整;
(3)请你仿照小明的方法将乙城市16台自动售货机的销售情况表示出来.
相关试题

