搜索
【题目】一个正方形和两个等边三角形的位置如图所示，若∠3=50°，则∠1+∠2=（ ）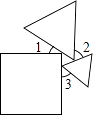 
A.90°
B.100°
C.130°
D.180°
参考答案：
【答案】B
【解析】解：如图，∠BAC=180°﹣90°﹣∠1=90°﹣∠1， ∠ABC=180°﹣60°﹣∠3=120°﹣∠3，
∠ACB=180°﹣60°﹣∠2=120°﹣∠2，
在△ABC中，∠BAC+∠ABC+∠ACB=180°，
∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°，
∴∠1+∠2=150°﹣∠3，
∵∠3=50°，
∴∠1+∠2=150°﹣50°=100°．
故选：B．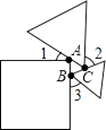
设围成的小三角形为△ABC，分别用∠1、∠2、∠3表示出△ABC的三个内角，再利用三角形的内角和等于180°列式整理即可得解．
-
科目： 来源： 题型：
查看答案和解析>>【题目】顺次连接菱形各边的中点所形成的四边形是（ ）
A.等腰梯形
B.矩形
C.菱形
D.正方形 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC在直角坐标系中，
（1）请写出△ABC各点的坐标；
（2）求出S△ABC；
（3）若把△ABC向上平移2个单位，再向右平移2个单位得△A′B′C′，在图中画出△ABC变化位置，并写出A′、B′、C′的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AB∥CD，∠ABC=∠ADC，DE垂直于对角线AC，垂足是E，连接BE．
（1）求证：四边形ABCD是平行四边形；
（2）若点E是AC的中点，判断BE与AC的位置关系，并说明理由；
（3）若△ABE是等边三角形，AD=
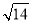，求对角线AC的长．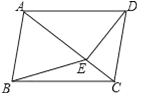
-
科目： 来源： 题型：
查看答案和解析>>【题目】某体育用品专卖店销售7个篮球和9个排球的总利润为355元，销售10个篮球和20个排球的总利润为650元．
（1）求每个篮球和每个排球的销售利润；
（2）已知每个篮球的进价为200元，每个排球的进价为160元，若该专卖店计划用不超过17400元购进篮球和排球共100个，且要求篮球数量不少于排球数量的一半，请你为专卖店设计符合要求的进货方案． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：一次函数
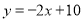的图象与反比例函数
（
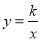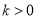）的图象相交于A，B两点（A在B的右侧）．（1）当A（4，2）时，求反比例函数的解析式及B点的坐标；
（2）在（1）的条件下，反比例函数图象的另一支上是否存在一点P，使△PAB是以AB为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
（3）当A（a，﹣2a+10），B（b，﹣2b+10）时，直线OA与此反比例函数图象的另一支交于另一点C，连接BC交y轴于点D．若
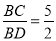，求△ABC的面积．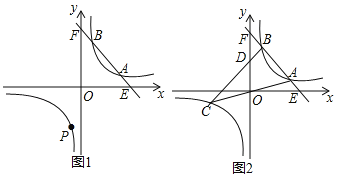
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，ABCD的对角线AC、BD交于点O，EF过点O且与BC、AD分别交于点E、F．试猜想线段AE、CF的关系，并说明理由．
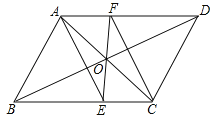
相关试题
