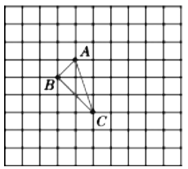
【题目】如图,正方形网格中的![]() ,若小方格边长为1,格点三角形(顶点是网格线的交点的三角形)
,若小方格边长为1,格点三角形(顶点是网格线的交点的三角形)![]() 的顶点
的顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)作出三角形![]() 关于y 轴对称的三角形
关于y 轴对称的三角形![]() ;
;
(3)判断![]() 的形状.
的形状.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() 是直角三角形.
是直角三角形.
【解析】
(1)根据点A、C的坐标确定原点的位置,然后建立坐标系即可;
(2)分别找到A、B、C关于y轴的对称点![]() ,然后连接
,然后连接![]() 、
、![]() 、
、![]() 即可;
即可;
(3)根据勾股定理分别求出AB、BC和AC的长,然后根据勾股定理的逆定理即可得出结论.
解:(1)∵点A![]() ,点C
,点C![]()
∴将点A向右平移1个单位,再向下平移1个单位或点C向上平移两个单位即可找到原点,
然后建立直角坐标系,如图所示:平面直角坐标系即为所求.

(2)分别找到A、B、C关于y轴的对称点![]() ,然后连接
,然后连接![]() 、
、![]() 、
、![]() ,如图所示,
,如图所示,![]() 即为所求;
即为所求;
(3)∵正方形小方格边长为1,
![]() ,
,
![]() ,
,
![]() 网格中的
网格中的![]() 是直角三角形.
是直角三角形.
-
科目: 来源: 题型:
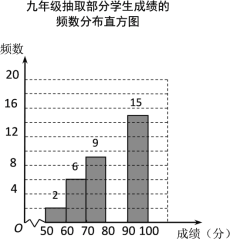
查看答案和解析>>【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
成绩x/分
频数
频率
第1段
x<60
2
0.04
第2段
60≤x<70
6
0.12
第3段
70≤x<80
9
b
第4段
80≤x<90
a
0.36
第5段
90≤x≤100
15
0.30
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)样本中,部分学生成绩的中位数落在第_______段;
(4)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )

A.
 B.
B.  C.
C.  D.
D. 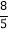
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有2个,若从中随机摸出一个球,这个球是白球的概率为
 .
.(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC.
(注:顶点在网格线交点处的三角形叫做格点三角形)
(1)图中AB的长为_________个单位长度;
(2)只用没有刻度的直尺,按如下要求画图:
① 以点C为位似中心,作△DEC∽△ABC,且相似比为1∶2;
②若点B为原点,点A(1,3),请在图2中画出平面直角坐标系,直接出△ABC的外心的坐标______________

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.

相关试题

