【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,当一点到达终点时,另一点也停止运动.设运动时间为x秒,△PBQ的面积为y(cm2). 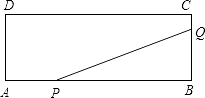
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
参考答案:
【答案】
(1)解:∵S△PBQ= ![]() PBBQ,PB=AB﹣AP=18﹣2x,BQ=x,
PBBQ,PB=AB﹣AP=18﹣2x,BQ=x,
∴y= ![]() (18﹣2x)x,
(18﹣2x)x,
即y=﹣x2+9x(0<x≤4)
(2)解:由(1)知:y=﹣x2+9x,
∴y=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∵当0<x≤ ![]() 时,y随x的增大而增大,
时,y随x的增大而增大,
而0<x≤4,
∴当x=4时,y最大值=20,
即△PBQ的最大面积是20cm2
【解析】(1)分别表示出PB、BQ的长,然后根据三角形的面积公式列式整理即可得解;(2)把函数关系式整理成顶点式解析式,然后根据二次函数的最值问题解答.
【考点精析】关于本题考查的二次函数的最值和矩形的性质,需要了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.
小明做了如下操作:
将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:
(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;
(2)连接EF,CD,如图③,求证:四边形CDEF是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系(如图1),y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
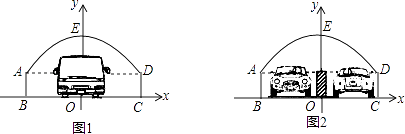
(1)求抛物线的解析式;
(2)现有一辆货运卡车,高4.4m,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双向道(如图2),为了安全起见,在隧道正中间设有0.4m的隔离带,则该辆货运卡车还能通过隧道吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.

(1)作出△ABC关于x轴对称的△A1B1C1 , (只画出图形).
(2)作出△ABC关于原点O成中心对称的△A2B2C2 , (只画出图形),写出B2和C2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售每个进价为150元和120元的A、B两种型号的足球,如表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3个
4个
1200元
第二周
5个
3个
1450元
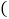 进价、售价均保持不变,利润
进价、售价均保持不变,利润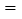 销售收入
销售收入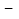 进货成本
进货成本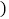
(1)求A、B两种型号的足球的销售单价;
(2)若商场准备用不多于8400元的金额再购进这两种型号的足球共60个,求A种型号的足球最多能采购多少个?
(3)在
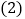 的条件下,商场销售完这60个足球能否实现利润超过2550元,若能,请给出相应的采购方案;若不能请说明理由.
的条件下,商场销售完这60个足球能否实现利润超过2550元,若能,请给出相应的采购方案;若不能请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF.请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可).
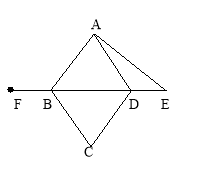
(1)连接 ;
(2)猜想: = ;
(3)证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列关系错误的是( )

A. ∠AOC=∠AOB+∠BOC
B. ∠AOC=∠AOD-∠COD
C. ∠AOC=∠AOB+∠BOD-∠BOC
D. ∠AOC=∠AOD-∠BOD+∠BOC
相关试题

