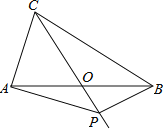
【题目】如图,在等腰△ABC中,AB=BC=4,点O是AB的中点,∠AOC=60°,点P是射线CO上的一个动点,若当△PAB为直角三角线时,试画出可能的图形(两种即可),并求出相应图形中的AP的长.
参考答案:
【答案】见解析
【解析】
试题分析:利用分类讨论,当∠APB=90°时,分两种情况讨论,情况一:易得∠PAB=30°,利用锐角三角函数得AP的长;情况二:如图2,利用直角三角形斜边的中线等于斜边的一半得出结论;当∠ABP=90°时,如图3易得BP,利用勾股定理可得AP的长;.
解:当∠APB=90°时,分两种情况.
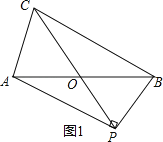
情况一:如图1,
∵AO=BO,
∴PO=BO,
∵∠AOC=60°,
∴∠BOP=60°,
∴△BOP为等边三角形,
∵AB=BC=4,
∴AP=ABsin60°=4×![]() =2
=2![]() ;
;
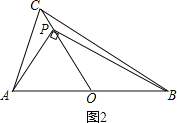
情况二:如图2,
∵AO=BO,∠APB=90°,
∴PO=AO,
∵∠AOC=60°,
∴△AOP为等边三角形,
∴AP=AO=2,
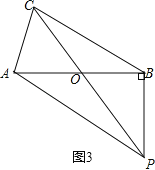
当∠ABP=90°时,如图3,
∵∠AOC=∠BOP=60°,
∴∠BPO=30°,
∴BP=![]() OB=2
OB=2![]() ,
,
在直角三角形ABP中,
AP=![]() =2
=2![]() ,
,
综上所述,AP的长为2![]() 或2
或2![]() 或2.
或2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(1,m),(2,n)在函数y=-x+1的图象上,则m、n的大小关系是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】梯形ABCD中,AD∥BC,AB=DC=2
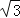 ,∠DBC=30°,∠BDC=90°,求:梯形ABCD的面积.
,∠DBC=30°,∠BDC=90°,求:梯形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两点在数轴上的位置如图所示,其中点A对应的有理数为-4,且AB=10。动点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒(t>0)。

(1)当t=1时,AP的长为_________,点P表示的有理数为______;
(2)当PB=2时,求t的值;
(3)M为线段AP的中点,N为线段PB的中点. 在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2a-b=5,a-2b=4,则a-b的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣a3b) 2的结果是( )
A. a5b2 B. ﹣a3b2 C. 2a6b2 D. a6b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求∠CDE的余弦值.

相关试题

