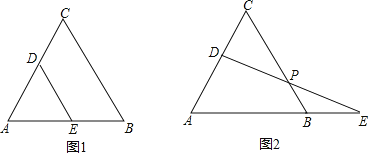
【题目】如图,D为等边△ABC的边AC上一点,E为直线AB上一点,CD=BE.
(1)如图1,求证;AD=DE;
(2)如图2,DE交CB于点P.
①若DE⊥AC,PC=6,求BP的长;
②猜想PD与PE之间的数量关系,并证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)①BP=3;②PD=PE,理由见解析.
【解析】
(1)只要证明△ADE是等边三角形即可;
(2)①利用直角三角形30度角性质即可解决问题;②过点D作DQ∥AB交BC于点Q,只要证明△CDQ是等边三角形,△DQP≌△EBP(AAS)即可解决问题.
(1)∵△ABC是等边三角形,
∴AB=AC,∠A=60°,
∵CD=BE,
∴AB-BE=AC-CD,即AD=AE,
∵∠A=60°,
∴△ADE是等边三角形.
∴AD=DE.

(2)①∵DE⊥AC,∠A=60°,
∴∠E=30°,
∵∠ABC=60°,
∴∠E=∠BPE=30°=∠CPD,
∴BP=BE,CD=![]() PC=3,
PC=3,
∵CD=BE,
∴BP=BE=3.
②PD=PE,理由如下:
如图2,过点D作DQ∥AB,交BC于点Q,
∴∠CDQ=∠A=60°,∠CQD=∠ABC=60°,∠DQP=∠EBP,
∴△DCQ是等边三角形,
∴DQ=CD=BE.
∵∠DPQ=∠EPB,∠DQP=∠EBP,
∴△DQP≌△EBP,
∴PD=PE.
-
科目: 来源: 题型:
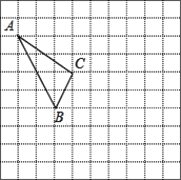
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为A(-4,5),C(-1,3).
(1)请在如图所示的网格内作出x轴、y轴;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标并求出△A1B1C1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,证明:AB=FA+BD;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】多好佳水果店在批发市场购买某种水果销售,第一次用1500元购进若干千克,并以每千克9元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1694元所购买的水果比第一次多20千克,以每千克10元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价45%售完剩余的水果.
(1)第一次水果的进价是每千克多少元?
(2)该水果店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A(-2,0),B(0,6),C(6,0),∠ABC+∠ADC=180°,BC⊥CD.
(1)求证:∠ABO=∠CAD;
(2)求四边形ABCD的面积;
(3)如图2,E为∠BCO的邻补角的平分线上的一点,且∠BEO=45°,OE交BC于点F,求BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 边长为
边长为 的等边三角形
的等边三角形 的顶点
的顶点 分别在边
分别在边 ,
, 上当
上当 在边
在边 上运动时,
上运动时, 随之在边
随之在边 上运动,等边三角形的形状保持不变,运动过程中,点
上运动,等边三角形的形状保持不变,运动过程中,点 到点
到点 的最大距离为( )
的最大距离为( ) 
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,每个小正方形边长都是1.
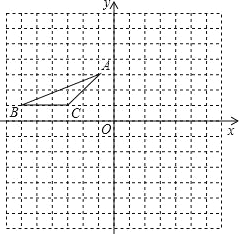
(1)按要求作图:
①△ABC关于x轴对称的图形△A1B1C1;
②将△A1B1C1向右平移7个单位得到△A2B2C2.
(2)回答下列问题:
①△A2B2C2中顶点B2坐标为 .
②若P(a,b)为△ABC边上一点,则按照(1)中①、②作图,点P对应的点P2的坐标为 .
相关试题

