【题目】树人学校实施新课程改革以来,学生的学习能力有了很大提高.周老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:

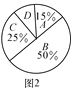
(1)本次调查中,周老师一共调查了________名学生,扇形统计图中“较差”部分的圆心角是__________;
(2)将条形统计图补充完整;
(3)如果树人学校共有6000名学生,“特别好”的有多少人?
参考答案:
【答案】(1)20,36°;(2)详见解析;(3)900.
【解析】试题分析:(1)用特别好的学生人数除以特别好的学生人数所占的百分比即可得这次调查的学生人数;根据扇形统计图求得较差学生所占的百分比,用360°乘以较差学生所占的百分比即可;(2)求得一般和较差学生的人数,再求得一般学生中的女生人数和较差学生中的男生人数,补全统计图即可;(3)用总人数乘以特别好学生所占的百分比即可.
试题解析:
(1)(2+1)÷15%=20(人);
360°×(1-50%-25%-15%)=36°;
故答案为:20,36°;
(2)20×25%=5(人),5-2=3人;
20×(1-50%-25%-15%)=2(人),2-1=1人;
补图如下:
(3)6000×15%=900(人),
答:“特别好”的有900人.
-
科目: 来源: 题型:
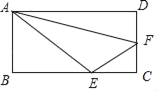
查看答案和解析>>【题目】如图,点E、F分别在矩形ABCD的边BC和CD上,如果△ABE、△ECF、△FDA的面积分别刚好为6、2、5,那么矩形ABCD的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三支排球队共同参加一届比赛,由抽签决定其中两队先打一场,然后胜者再和第三队(第一场轮空者)比赛,争夺冠军.
(1)如果采用在暗盒中放形状大小完全一致的两黑一白三个小球,摸到白色小球的第一场轮空直接晋级进入决赛,那么甲队摸到白色小球的概率是多少?
(2)如果采用三队各抛一枚硬币,当出现二正一反或二反一正时则由抛出同面的两个队先打一场,而出现三枚同面(同为正面或反面)时,则重新抛,试用“树形图”或表格表示第一轮抽签(抛币)所有可能的结果,并指出必须进行第二轮抽签的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy 中,点A 的坐标为(1,0),P 是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).若点P到x轴的距离为
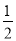 ,则m+n 的最小值为___.
,则m+n 的最小值为___. -
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑摩托车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B 村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
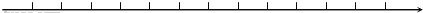
(2)C村离A村有多远?
(3)若摩托车每100km耗油3升,这趟路共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校召集留守儿童过端午节,桌上摆有甲、乙两盘粽子,每盘中盛有白粽2个,豆沙粽1个,肉粽1个(粽子外观完全一样).
(1)小明从甲盘中任取一个粽子,取到豆沙粽的概率是 ;
(2)小明在甲盘和乙盘中先后各取了一个粽子,请用树状图或列表法求小明恰好取到两个白粽子的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB∥CD,AD=BC,∠B=60°,AC平分∠DAB.
(1)求∠ACB的度数;
(2)如果AD=1,请直接写出向量
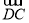 和向量
和向量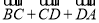 的模.
的模.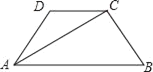
相关试题

