搜索
【题目】校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道
上确定点D，使CD与垂直，测得CD的长等于21米，在上点D的同侧取点A、B，使∠CAD=300，∠CBD=600．
(1)求AB的长(精确到0.1米，参考数据：
)；
(2)已知本路段对校车限速为40千米／小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速?说明理由．
参考答案：
【答案】（1）24.2米(2) 超速，理由见解析
【解析】解：（1）由題意得，
在Rt△ADC中，
，
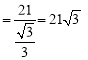在Rt△BDC中，
，
∴AB=AD－BD= 
（米）。
（2）∵汽车从A到B用时2秒，∴速度为24.2÷2=12.1（米/秒），
∵12.1米/秒=43.56千米/小时，∴该车速度为43.56千米/小时。
∵43.56千米/小时大于40千米/小时，∴此校车在AB路段超速。
（1）分别在Rt△ADC与Rt△BDC中，利用正切函数，即可求得AD与BD的长，从而求得AB的长。
（2）由从A到B用时2秒，即可求得这辆校车的速度，比较与40千米/小时的大小，即可确定这辆校车是否超速。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，反比例函数y=
（x＞0）的图象交矩形OABC的边AB于点D，交BC于点E，且BE=2EC，若四边形ODBE的面积为8，则k=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图在ABCD中，点E为AB上一点，连接CE、DE，且CE⊥AB，CE＝AB，点F为BC上一点，连接DF交CE于点G，∠CGD＝∠B；
（1）若CG＝2，AD＝3，求GE的长；
（2）若CF＝
DE，求证：AD＝CG+BE． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，∠ABC=60°，AB=6cm，将△ABC以点B为中心顺时针旋转，使点C旋转到AB边延长线上的点D处，则AC边扫过的图形（阴影部分）的面积是_____cm2．（结果保留π）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学九（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：
（1）九（1）班的学生人数为 ，并把条形统计图补充完整；
（2）扇形统计图中m= ，n= ，表示“足球”的扇形的圆心角是 度；
（3）排球兴趣小组4名学生中有3男1女，现在打算从中随机选出2名学生参加学校的排球队，请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点G是正方形ABCD对角线CA的延长线一点，对角线BD与AC交于点O，以线段AG为边作一个正方形AEFG，连接EB、GD．
（1）求证：EB=GD；
（2）若AB=5，AG=2
，求EB的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于给定的函数，自变量取x1，x2时，对应的函数值分别记为y1，y2．自变量取
时．对应的函数值记为
，例如一次函数y＝2x+1，自变量取x1，x2时，对应的函数值分别为y1＝2x1+1，y2＝2x2+1，自变量取时，对应的函数值为＝2+1，若对于给定的函数，自变量取x1，x2（x1≠x2）时，总有
，则称函数为凸凸函数．对于给定的函数总有
，则称函数为凹凹函数．对于给定的函数总有
，则称函数为平平函数．（1）求证：函数y＝2x是平平函数；
（2）判断函数y＝ax2是凸凸函数，凹凹函数还是平平函数．
相关试题
