【题目】某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:
原进价(元/个) | 零售价(元/个) | 成套售价(元/套) | |
螺丝 | a | 1.0 | 2.0 |
螺母 | a﹣0.3 | 0.6 | 2.0 |
(1)已知用50元购进螺丝的数量与用20元购进螺母的数量相同,求表中a的值;
(2)若该店购进螺母数量是螺丝数量的3倍还多200个,且两种配件的总量不超过3000个.
①该店计划将一半的螺丝配套(一个螺丝和两个螺母配成一套)销售,其余螺丝、螺母以零售方式销售.请问:怎样进货,才能获得最大利润?最大利润是多少?(用含a的代数式表示)
②由于原材料价格上涨,每个螺丝和螺母的进价都上涨了0.1元.按照①中的最佳进货方案,在销售价不变的情况下,全部售出后,所得利润比①少了260元,请问本次成套的销售量为多少?

参考答案:
【答案】(1)a=0.5;(2)①购进螺丝700个,购进螺母2300,利润为2700-3000a;②成套的销售量为150套
【解析】分析:(1)根据用50元购进螺丝的数量与用20元购进螺母的数量相同找出等量关系列方程求解,解分式方程要验根;
(2)①设购进螺丝x个,则购进螺母(3x+200)个,根据两种配件的总量不超过3000个列不等式求出x的取值范围;然后根据总利润=成套卖的利润+单卖螺丝的利润+单卖螺母的利润列出一次函数关系式求解;②设成套的销售量为m套,则零售的螺丝为(700﹣m)个,零售的螺母为(2300﹣2m)个,结合①中求得最大利润列方程求解.
详解:(1)依题意得![]() a=0.5,
a=0.5,
经检验:a=0.5是原方程的解,且符合题意.
(2)①设购进螺丝x个,则购进螺母(3x+200)个,依题意得
x+(3x+200)≤3000,
x≤700,
则成套的卖出时利润为:![]() x[2﹣a﹣2(a﹣0.3)]元;单个螺丝的利润为:
x[2﹣a﹣2(a﹣0.3)]元;单个螺丝的利润为:![]() x(1﹣a);
x(1﹣a);
单个螺母的利润为:(3x+200﹣x)[0.6﹣(a﹣0.3)],
设利润为y元,则![]() ,
,
=(3.6﹣4a)x+(180﹣200a).
解法一:
由已知得![]() ,
,
解得a<0.9.
∵当a<0.9时,k=3.6﹣4a>0,
∴函数y=(3.6﹣4a)x+(180﹣200a)中的y随x增大而增大.
∴当x=700时,y最大=2700﹣3000a.
解法二:
分两种情况讨论:
当3.6﹣4a>0,即a<0.9时,函数y=(3.6﹣4a)x+(180﹣200a)中的y随x增大而增大.
∴当x=700时,y最大=2700﹣3000a,
当3.6﹣4a≤0时,a≥0.9.
∵根据成套销售价应高于成本价可得:a+2(a﹣0.3)≤2,即a≤![]() ,
,
∴此时不符合题意,舍去.
②设成套的销售量为m套,则零售的螺丝为(700﹣m)个,零售的螺母为(2300﹣2m)个,依题意得:
m[2﹣a﹣2(a﹣0.3)﹣0.3]+(700﹣m)(1﹣a﹣0.1)+(2300﹣2m)[0.6﹣(a﹣0.3)﹣0.1]=﹣0.2m﹣3000a+2470,
故:﹣0.2m﹣3000a+2470=2700﹣3000a﹣260,
解得:m=150,
故成套的销售量为150套.
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇准备完成题目:化简:
 ,发现系数“
,发现系数“ ”印刷不清楚.
”印刷不清楚.(1)他把“
 ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“
 ”是几?
”是几? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABD中,边AB=OB=1,∠ABO=90°
问题探究:
(1)以AB为边,在Rt△ABO的右边作正方形ABC,如图(1),则点O与点D的距离为 .
(2)以AB为边,在Rt△ABO的右边作等边三角形ABC,如图(2),求点O与点C的距离.
问题解决:
(3)若线段DE=1,线段DE的两个端点D,E分别在射线OA、OB上滑动,以DE为边向外作等边三角形DEF,如图(3),则点O与点F的距离有没有最大值,如果有,求出最大值,如果没有,说明理由.
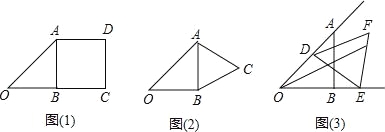
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)若半圆O的半径为6,求
 的长.
的长.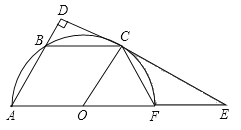
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(
 ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=
 AE;
AE;(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2
 ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,各情况分别可以和哪幅画来近似刻画?

(1)一个球被向上抛起,直到落到地面的过程(球的高度与时间的关系) ;
(2)常温下,往一杯凉水中倒开水(水温与时间的关系) ;
(3)将澡盆中的水放掉(水的高度与时间的关系)
相关试题

