【题目】
(1)如图1,点P是ABCD内的一点,分别过点B、C、D作AP的垂线BE、CF、DH,垂足分别为E、F、H,猜想BE、CF、DH三者之间的关系,并证明;
(2)如图2,若点P在ABCD的外部,△APB的面积为18,△APD的面积为3,求△APC的面积;
(3)如图3,在(2)的条件下,增加条件:AB=BC,∠APC=ABC=90°,设AP、BP分别于CD相交于点M、N,当DM=CN时, ![]() =(请直接写出结论).
=(请直接写出结论).
参考答案:
【答案】
(1)
解:过C作CG⊥BE于G,延长BC交AF于Q,

∵CF⊥AC,BE⊥AC,
∴四边形CGEF是矩形,
∴EG=CF,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAH=∠Q,
∵CG∥AF,
∴∠G=∠BCG,
∴∠DAH=∠BCG,
在△ADH与△BCG中,  ,
,
∴△ADH≌△BCG,
∴DH=BG,
∴BE=BG+EG=DH+CF
(2)
解:分别过点B、C、D作AP的垂线BE、CF、DH,垂足分别为E、F、H,

由(1)知BE=DH+CF,
∵S△ADP= ![]() APDH,S△ABP=
APDH,S△ABP= ![]() APBE,S△ACP=
APBE,S△ACP= ![]() APCF,
APCF,
∴S△ADP+S△ACP= ![]() AP(DH+CF)=
AP(DH+CF)= ![]() APBE=S△ABP,
APBE=S△ABP,
∵△APB的面积为18,△APD的面积为3,
∴S△APC=15;
(3)![]()
【解析】解:(3)过B作BE⊥AP于E,连接AC,
∵AB=BC,∠ABC=90°,
∴四边形ABCD是正方形,
∴∠DCA=∠CAB=45°,
在△ADM与△BCN中,  ,
,
∴△ADM≌△BCN,
∴AM=BN,∠AMD=∠BNC,
∴∠PMN=∠PNM,
∴PM=PN,
∴AP=BP,
∵∠ADC=∠APC=90°,
∴A,C,P,D四点共圆,
∴∠DPA=∠ACD=45°,
在△PDM与△PCN中,  ,
,
∴△PDM≌△PCN,
∴∠CPN=∠DPM=45°,
∴∠APB=45°,
∴△BPE是等腰直角三角形,
∴PB=PA= ![]() BE,
BE,
∵S△ABP= ![]() APBE=
APBE= ![]() ×
× ![]() BEBE=18,
BEBE=18,
∴BE=3 ![]() ,
,
∴AP=6 ![]() ,
,
∵APPC=30,
∴PC= ![]() ,
,
∵∠PDC=∠PCD=∠PAC,
∴tan∠PCM=tan∠PAC= ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用三角形的面积对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知sinβ=0.8290,则β的度数约为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 2a +3b = 5ab B. a2·a3=a5 C. (2a) 3 = 6a3 D. a6+a3= a9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列说法正确的是( )

A.若AB∥DC,则∠1=∠2
B.若AD∥BC,则∠3=∠4
C.若∠1=∠2,则AB∥DC
D.若∠2+∠3+∠A=180°,则AB∥DC -
科目: 来源: 题型:
查看答案和解析>>【题目】若x<-2,则下列不等式成立的是( )
A. x2>-2x B. x2≥-2x C. x2<-2x D. x2≤-2x
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,若EG平分∠BEF,FM平分∠EFD交EG于M,EN平分∠AEF,则与∠FEM互余的角有( )
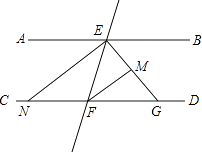
A.3个
B.4个
C.5个
D.6个 -
科目: 来源: 题型:
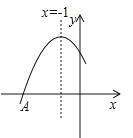
查看答案和解析>>【题目】如图是二次函数
 图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论:
图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论:①abc<0,②
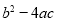 >0,③4b+c<0,④若B(
>0,③4b+c<0,④若B( ,
,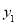 )、C(
)、C(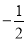 ,
, )为函数图象上的两点,则
)为函数图象上的两点,则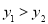 ,⑤当﹣3≤x≤1时,y≥0.
,⑤当﹣3≤x≤1时,y≥0.其中正确的结论是(填写代表正确结论的序号) .
相关试题

