Question

【题目】如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．

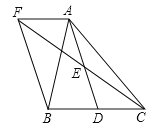
（1）线段BD与CD有什么数量关系，并说明理由；

（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．

Answer 1

【答案】（1）BD=CD.理由见解析；（2）当△ABC满足：AB=AC时，四边形AFBD是矩形．理由见解析.

【解析】

试题分析：（1）根据两直线平行，内错角相等求出∠AFE=∠DCE，然后利用“角角边”证明△AEF和△DEC全等，根据全等三角形对应边相等可得AF=CD，再利用等量代换即可得证；

（2）先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形，再根据一个角是直角的平行四边形是矩形，可知∠ADB=90°，由等腰三角形三线合一的性质可知必须是AB=AC．

试题解析：（1）BD=CD．

理由如下：依题意得AF∥BC，

∴∠AFE=∠DCE，

∵E是AD的中点，

∴AE=DE，

在△AEF和△DEC中，

，

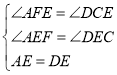∴△AEF≌△DEC（AAS），

∴AF=CD，

∵AF=BD，

∴BD=CD；

（2）当△ABC满足：AB=AC时，四边形AFBD是矩形．

理由如下：∵AF∥BD，AF=BD，

∴四边形AFBD是平行四边形，

∵AB=AC，BD=CD（三线合一），

∴∠ADB=90°，

∴AFBD是矩形．