搜索
【题目】（1）
﹣（+9）﹣12﹣（
）
（2）4﹣2×（﹣3）2+6÷（﹣
）
（3）化简：5（a2+5a）﹣（a2+7a）
（4）先化简，再求值：2（a2b+ab2）﹣3（a2b﹣1）﹣2ab2﹣4，其中a＝2018，b＝
．
参考答案：
【答案】（1）
；（2）﹣26；（3）4a2+18a；（4）﹣a2b﹣1；﹣2019.
【解析】
（1）根据有理数加减法法则计算即可；（2）根据有理数混合运算法则计算即可；（3）先去括号，再根据合并同类项法则计算化简即可；（4）先去括号，再根据合并同类项法则化简，然后代入a、b的值计算即可.
（1）原式＝
﹣
﹣21
＝
﹣21
＝
；
（2）原式＝4﹣2×9﹣6×2
＝4﹣18﹣12
＝﹣14﹣12
＝﹣26；
（3）原式＝5a2+25a﹣a2﹣7a
＝4a2+18a；
（4）原式＝2a2b+2ab2﹣3a2b+3﹣2ab2﹣4
＝﹣a2b﹣1，
当a＝2018，b＝
时，
原式＝﹣20182×﹣1
＝﹣2018﹣1
＝﹣2019.
-
科目： 来源： 题型：
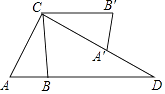
查看答案和解析>>【题目】如图，在△ABC中，AB=3，AC=6，将△ABC绕点C按逆时针方向旋转得到△A1B1C，使CB1∥AD，分别延长AB、CA1相交于点D，则线段BD的长为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小美周末来到公园，发现在公园一角有一种“守株待兔”游戏．游戏设计者提供了一只兔子和一个有A，B，C，D，E五个出入口的兔笼，而且笼内的兔子从每个出入口走出兔笼的机会是均等的．规定：①玩家只能将小兔从A，B两个出入口放入，②如果小兔进入笼子后选择从开始进入的出入口离开，则可获得一只价值5元小兔玩具，否则每玩一次应付费3元．
（1）请用表格或树状图求小美玩一次“守株待兔”游戏能得到小兔玩具的概率；
（2）假设有1000人次玩此游戏，估计游戏设计者可赚多少元？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图,一个正比例函数图象与一个一次函数图象交于点A(3,4),且一次函数的图象与y轴相交于点B(0,-5).
(1)求这两个函数的表达式;
(2)求△AOB的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小区规划一个长70m、宽30m的长方形草坪上修建三条同样宽的甬道，使其中两条与AB平行，另一条与BC平行，场地其余部分种草，甬道的宽度为xm．
（1）用含x的代数式表示草坪的总面积S；
（2）如果每一块草坪的面积都相等，且甬道的宽为1m，那么每块草坪的面积是多少平方米？（精确到0.1）
-
科目： 来源： 题型：
查看答案和解析>>【题目】一水果经销商购进了A，B两种水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售，预计每箱水果的盈利情况如下表：
A种水果/箱
B种水果/箱
甲店
11元
17元
乙店
9元
13元
（1）如果甲、乙两店各配货10箱，其中A种水果两店各5箱，B种水果两店各5箱，请你计算出经销商能盈利多少元？
（2）在甲、乙两店各配货10箱（按整箱配送），且保证乙店盈利不小于100元的条件下，请你设计出使水果经销商盈利最大的配货方案，并求出最大盈利为多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处，某校数学课外兴趣小组的同学正在测量旗杆的高度，在旗杆的底部A处测得点D的仰角为15°，AC=10米，又测得∠BDA=45°．已知斜坡CD的坡度为i=1：
，求旗杆AB的高度（ 
，结果精确到个位）．
相关试题
