【题目】如图,一个正比例函数图象与一个一次函数图象交于点A(3,4),且一次函数的图象与y轴相交于点B(0,-5).

(1)求这两个函数的表达式;
(2)求△AOB的面积.
参考答案:
【答案】(1) y=![]() x. y=3x-5;(2) 7.5
x. y=3x-5;(2) 7.5
【解析】试题分析:(1)利用待定系数法,将A,B两点分别代入求出即可;
(2)△AOB的高是点A的横坐标3,底边是线段OB的长,所以利用函数解析式求出与y轴交点坐标,从而求出面积,
试题解析:(1)设直线OA对应的函数表达式是y=kx.
因为直线y=kx经过点(3,4),
所以3k=4,k=![]() .所以y=
.所以y=![]() x.
x.
设直线AB对应的函数表达式是y=kx+b,
因为直线y=kx+b经过(3,4),(0,-5),
所以b=-5,3k+b=4.所以k=3,b=-5.
所以y=3x-5.
(2)S△AOB=![]() ×5×3=7.5.
×5×3=7.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形的长为2a+3b,宽为2b,则它的面积为_________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别
A型
B型
AB型
O型
频率
0.4
0.35
0.1
0.15
A.16人
B.14人
C.4人
D.6人 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系
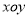 中,一次函数
中,一次函数 的图象与反比例函数
的图象与反比例函数 的图象交于
的图象交于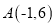 、
、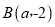 两点.
两点.
(1)求一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)当
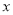 满足________________时,
满足________________时, 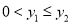 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)求出线段AB,曲线CD的解析式,并写出自变量的取值范围;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程(x+6)2=16可转化为两个一元一次方程,其中一个一元一次方程是x+6=4,则另一个一元一次方程是( )
A.x﹣6=﹣4
B.x﹣6=4
C.x+6=4
D.x+6=﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=ax2的图象经过点P(﹣2,4),则该图象必经过点( )
A.(2,4)
B.(﹣2,﹣4)
C.(﹣4,2)
D.(4,﹣2)
相关试题

