搜索
【题目】如图，△ABC内接于⊙O，且AB为⊙O的直径，OD⊥AB，与AC交于点E，与过点C的⊙O的切线交于点D．
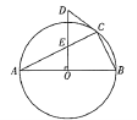
（1）若AC=4，BC=2，求OE的长．
（2）试判断∠A与∠CDE的数量关系，并说明理由．
参考答案：
【答案】（1）
；（2）∠CDE=2∠A．
【解析】
试题分析：（1）在Rt△ABC中，由勾股定理得到AB的长，从而得到半径AO ．再由△AOE∽△ACB，得到OE的长；
（2）连结OC，得到∠1=∠A，再证∠3=∠CDE，从而得到结论．
试题解析：（1）∵AB是⊙O的直径，∴∠ACB=90°，在Rt△ABC中，由勾股定理得：AB=
=
=
，∴AO=
AB=
．∵OD⊥AB，∴∠AOE=∠ACB=90°，又∵∠A=∠A，∴△AOE∽△ACB，∴
，∴OE=
=
=.
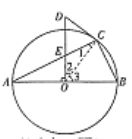
（2）∠CDE=2∠A．理由如下：
连结OC，∵OA=OC，∴∠1=∠A，∵CD是⊙O的切线，∴OC⊥CD，∴∠OCD=90°，∴∠2+∠CDE=90°，∵OD⊥AB，∴∠2+∠3=90°，∴∠3=∠CDE．∵∠3=∠A+∠1=2∠A，∴∠CDE=2∠A．
-
科目： 来源： 题型：
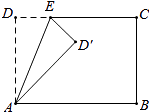
查看答案和解析>>【题目】如图，在矩形ABCD中，AD=5，AB=8，点E为DC边上的一个动点，把△ADE沿AE折叠，当点D的对应点刚好D落在矩形ABCD的对称轴上时，则DE的长为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学校举行了主题为“让历史照亮未来”的演讲比赛，其中代表七、八年级参赛的两队各10人的比赛成绩如下表（10分制）：
七年级队
7
8
9
7
10
10
9
10
10
10
八年级队
10
8
7
9
8
10
10
9
10
9
（1）请直接写出七年级队成绩的中位数为 ， 八年级队成绩的众数为；
（2）若七、八年级队的平均成绩均为9分，请分别计算七、八年级队的方差． -
科目： 来源： 题型：
查看答案和解析>>【题目】若a、b、c为三角形的三边长，且a、b满足|a﹣3|+（b﹣2）2=0，则第三边长c的取值范围是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合与探究
如图，抛物线
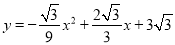与
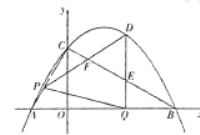
轴交于A、B两点（点A在点B的左侧），与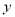
轴交于点C，连接AC、BC．点P沿AC以每秒1个单位长度的速度由点A向点C运动，同时，点Q沿BO以每秒2个单位长度的速度由点B向点O运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ，过点Q作QD⊥x轴，与抛物线交于点D，与BC交于点E．连接PD，与BC交于点F．设点P的运动时间为
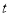秒（
）．
（1）求直线BC的函数表达式．
（2）①直接写出P、D两点的坐标（用含
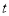的代数式表示，结果需化简）．②在点P、Q运动的过程中，当PQ=PD时，求
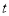的值．（3）试探究在点P、Q运动的过程中，是否存在某一时刻，使得点F为PD的中点．若存在，请直接写出此时
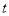的值与点F的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了准确反映某车队10名司机1月份耗去的汽油费用，且便于比较，那么选用最合适、直观的统计图是（ ）
A. 统计表B. 条形统计图C. 扇形统计图D. 折线统计图
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合与实践
背景阅读 早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三，股四，弦五”．它被记载于我国古代著名数学著作《周髀算经》中．为了方便，在本题中，我们把三边的比为3：4：5的三角形称为（3，4，5）型三角形．例如：三边长分别为9，12，15或
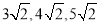的三角形就是（3，4，5）型三角形．用矩形纸片按下面的操作方法可以折出这种类型的三角形．实践操作 如图1，在矩形纸片ABCD中，AD=8cm，AB=12cm．
第一步：如图2，将图1中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平．
第二步：如图3，将图2中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF．
第三步：如图4，将图3中的矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM与折痕EF交于点N，然后展平．
问题解决
（1）请在图2中证明四边形AEFD是正方形．
（2）请在图4中判断NF与ND′的数量关系，并加以证明．
（3）请在图4中证明△AEN是（3，4，5）型三角形．
探索发现
（4）在不添加字母的情况下，图4中还有哪些三角形是（3，4，5）型三角形？请找出并直接写出它们的名称．
相关试题
