Question

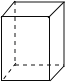
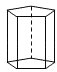
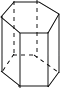
【题目】观察下列多面体,并把下表补充完整.

名称	三棱柱	四棱柱	五棱柱	六棱柱
图形
顶点数a	6		10	12
棱数b	9	12
面数c	5			8

（1）完成上表中的数据

（2）根据上表中的规律判断，十四棱柱共有　 　个面，共有　 　个顶点，共有　 　条棱；

（3）若某个棱柱由30个面构成，则这个棱柱为　 　棱柱；

（4）观察上表中的结果,你能发现顶点数棱数面数之间有什么关系吗?请写出来。

Answer 1

【答案】（1）填表见解析（2）十四棱柱共有16个面，共有28个顶点，共有42条棱；（3）这个棱柱为二十八棱柱；（4）关系：顶点数+面数﹣棱数=2．

【解析】试题分析：（1）结合三棱柱、四棱柱、五棱柱和六棱柱的特点，即可填表；

（2）找到规律，顶点数是2n，棱数是3n，面数是n+2，然后再代入求解即可；

（3）代入面数的规律n+2=30，即可求解；

（4）利用前面的规律得出顶点数、棱数、面数的关系即可.

试题解析：（1）填表如下：

名称	三棱柱	四棱柱	五棱柱	六棱柱
图形
顶点数a	6	8	10	12
棱数b	9	12	15	18
面数c	5	6	7	8

（2）根据上表中的规律判断，十四棱柱共有16个面，共有28个顶点，共有42条棱；

（3）若某个棱柱由30个面构成，则这个棱柱为二十八棱柱；

（4）关系：顶点数+面数﹣棱数=2．