【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣3,0)、B(5,0)、C(0,5)三点,O为坐标原点
(1)求此抛物线的解析式;
(2)若把抛物线y=ax2+bx+c(a≠0)向下平移![]() 个单位长度,再向右平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
个单位长度,再向右平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
(3)设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.

参考答案:
【答案】(1)y=﹣![]() x2+
x2+![]() x+5;(2)0<n<3;(3)PC的长为7或17.
x+5;(2)0<n<3;(3)PC的长为7或17.
【解析】
试题分析:(1)根据A、B、C三点的坐标,利用待定系数法可求得抛物线的解析式即可;(2)可先求得抛物线的顶点坐标,再利用坐标平移,可得平移后的坐标为(1+n,1),再由B、C两点的坐标可求得直线BC的解析式,可求得y=1时,对应的x的值,从而可求得n的取值范围;(3)当点P在y轴负半轴上和在y轴正半轴上两种情况,根据这两种情况分别求得PC的长即可.
试题解析:(1)把A、B、C三点的坐标代入函数解析式可得 ,
,
解得![]() ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+5;
x+5;
(2)∵y=﹣![]() x2+
x2+![]() x+5,
x+5,
∴抛物线顶点坐标为(1,![]() ),
),
∴当抛物线y=ax2+bx+c(a≠0)向下平移![]() 个单位长度,再向右平移n(n>0)个单位长度后,得到的新抛物线的顶点M坐标为(1+n,1),
个单位长度,再向右平移n(n>0)个单位长度后,得到的新抛物线的顶点M坐标为(1+n,1),
设直线BC解析式为y=kx+m,把B、C两点坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线BC的解析式为y=﹣x+5,
令y=1,代入可得1=﹣x+5,解得x=4,
∵新抛物线的顶点M在△ABC内,
∴1+n<4,且n>0,解得0<n<3,
即n的取值范围为0<n<3;
(3)当点P在y轴负半轴上时,如图1,过P作PD⊥AC,交AC的延长线于点D,
由题意可知OB=OC=5,
∴∠CBA=45°,
∴∠PAD=∠OPA+∠OCA=∠CBA=45°,
∴AD=PD,
在Rt△OAC中,OA=3,OC=5,可求得AC=![]() ,
,
设PD=AD=m,则CD=AC+AD=![]() +m,
+m,
∵∠ACO=∠PCD,∠COA=∠PDC,
∴△COA∽△CDP,
∴![]() ,即
,即![]() ,
,
解得m=![]() ,PC=17;
,PC=17;
可求得PO=PC﹣OC=17﹣5=12,
如图2,在y轴正半轴上截取OP′=OP=12,连接AP′,
则∠OP′A=∠OPA,
∴∠OP′A+∠OCA=∠OPA+∠OCA=∠CBA,
∴P′也满足题目条件,此时P′C=OP′﹣OC=12﹣5=7,
综上可知PC的长为7或17.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列多面体,并把下表补充完整.
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形




顶点数a
6
10
12
棱数b
9
12
面数c
5
8
(1)完成上表中的数据
(2)根据上表中的规律判断,十四棱柱共有 个面,共有 个顶点,共有 条棱;
(3)若某个棱柱由30个面构成,则这个棱柱为 棱柱;
(4)观察上表中的结果,你能发现顶点数棱数面数之间有什么关系吗?请写出来。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若四边形ABCD是⊙O的内接四边形,∠A=120°,则∠C的度数是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 直线AB和直线a不能是同一条直线 B. 射线AB和射线BA是两条射线
C. 线段AB和线段BA是两条线段 D. 直线AB和直线BA是两条直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段MN=10 cm,现有一点P满足PM+PN=20 cm.有下列说法:①点P必在线段MN上;②点P必在直线MN外;③点P必在直线MN上;④点P可能在直线MN上;⑤点P可能在直线MN外.其中正确的说法是( )
A. ①② B. ②③ C. ④⑤ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年6月15日是父亲节,某商店老板统计了这四年父亲节当天剃须刀销售情况,以下是根据该商店剃须刀销售的相关数据所绘制统计图的一部分.
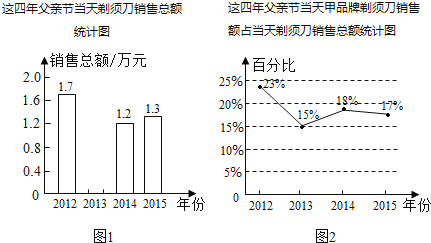
请根据图1、图2解答下列问题:
(1)近四年父亲节当天剃须刀销售总额一共是5.8万元,请将图1中的统计图补充完整;
(2)计算该店2015年父亲节当天甲品牌剃须刀的销售额.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的有( )个
①一条对角线平分一内角的平行四边形是菱形;
②两条对角线互相垂直的四边形是平行四边形;
③依次连接菱形各边中点得到的图形是正方形;
④两条对角线互相垂直且相等的四边形是正方形.
A.1B.2C.3D.4
相关试题

