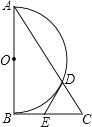
【题目】如图,ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.
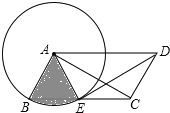
(1)求证:△AED≌△DCA;
(2)若DE平分∠ADC且与⊙A相切于点E,求图中阴影部分(扇形)的面积.
参考答案:
【答案】(1)见解析;(2)![]() π.
π.
【解析】
试题分析:(1)由四边形ABCD是平行四边形,AB=AE,易证得四边形AECD是等腰梯形,即可得AC=DE,然后由SSS,即可证得:△AED≌△DCA;
(2)由DE平分∠ADC且与⊙A相切于点E,可求得∠EAD的度数,继而求得∠BAE的度数,然后由扇形的面积公式求得阴影部分(扇形)的面积.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴四边形AECD是梯形,
∵AB=AE,
∴AE=CD,
∴四边形AECD是等腰梯形,
∴AC=DE,
在△AED和△DCA中,
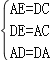 ,
,
∴△AED≌△DCA(SSS);
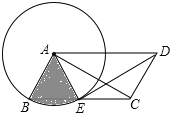
(2)解:∵DE平分∠ADC,
∴∠ADC=2∠ADE,
∵四边形AECD是等腰梯形,
∴∠DAE=∠ADC=2∠ADE,
∵DE与⊙A相切于点E,
∴AE⊥DE,
即∠AED=90°,
∴∠ADE=30°,
∴∠DAE=60°,
∴∠DCE=∠AEC=180°﹣∠DAE=120°,
∵四边形ABCD是平行四边形,
∴∠BAD=∠DCE=120°,
∴∠BAE=∠BAD﹣∠EAD=60°,
∴S阴影=![]() ×π×22=
×π×22=![]() π.
π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹣b=1,ab=﹣2,则(a﹣2)(b+2)=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式中,与﹣1+2相等的是( ).
A.2﹣1 B.﹣1﹣2 C.﹣(2﹣1) D.﹣(1+2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一个角是100°,则它的顶角是( )
A. 40° B. 60° C. 80° D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,4),与直线y=﹣x+1相交于A、B两点,其中点A在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).点M是直线AB上方的抛物线上一动点,过M作MP丄x轴,垂足为点P,交直线AB于点N,设点M的横坐标为m.
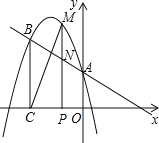
(1)求抛物线的解析式;
(2)当m为何值时,线段MN取最大值?并求出这个最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小洪根据演讲比赛中九位评委所给的分数制作了如下表格:
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( ).
A.平均数 B.中位数 C.众数 D.方差
相关试题

