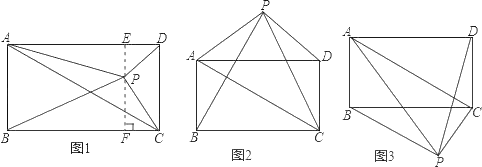
【题目】已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+S△PCD
理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
∵S△PBC+S△PAD=![]() BCPF+
BCPF+![]() ADPE=
ADPE=![]() BC(PF+PE)=
BC(PF+PE)=![]() BCEF=
BCEF=![]() S矩形ABCD.
S矩形ABCD.
(1)请补全以上证明过程.
(2)请你参考上述信息,当点P分别在图1、图2中的位置时,S△PBC、S△PAC、SPCD又有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明.
参考答案:
【答案】(1)证明见解析;(2)猜想结果:图2结论S△PBC=S△PAC+S△PCD; 图3结论S△PBC=S△PAC﹣S△PCD,证明见解析.
【解析】
分析图2,先过点P作EF垂直AD,分别交AD、BC于E、F两点,利用三角形的面积公式可知,经过化简,等量代换,可以得到S△PBC=S△PAD+![]() S矩形ABCD,而S△PAC+S△PCD=S△PAD+
S矩形ABCD,而S△PAC+S△PCD=S△PAD+![]() S矩形ABCD,故有S△PBC=S△PAC+S△PCD.
S矩形ABCD,故有S△PBC=S△PAC+S△PCD.
(1)证明:∵S△PAC+S△PCD+S△PAD=![]() S矩形ABCD,
S矩形ABCD,
∴S△PBC+S△PAD=S△PAC+S△PCD+S△PAD,
∴S△PBC=S△PAC+S△PCD;
(2)猜想结果:图2结论S△PBC=S△PAC+S△PCD; 图3结论S△PBC=S△PAC﹣S△PCD.
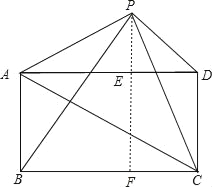
证明:如图,过点P作EF垂直AD,分别交AD、BC于E、F两点.
∵S△PBC=![]() BCPF=
BCPF=![]() BCPE+
BCPE+![]() BCEF
BCEF
=![]() ADPE+
ADPE+![]() BCEF=S△PAD+
BCEF=S△PAD+![]() S矩形ABCD
S矩形ABCD
S△PAC+S△PCD=S△PAD+S△ADC=S△PAD+![]() S矩形ABCD
S矩形ABCD
∴S△PBC=S△PAC+S△PCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学在一次测验中解答的填空题:
①若
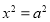 ,则
,则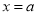 ;
;②方程
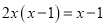 的解为
的解为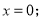
③已知三角形两边分别为2和9,第三边长是方程
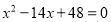 的根,则这个三角形的周长是17或19。
的根,则这个三角形的周长是17或19。其中答案完全正确的题目个数是_____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
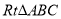 中,
中,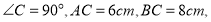 点P、Q同时由A、B两点出发,分别沿AC,BC的方向匀速运动,它们的速度都是每秒1cm,____秒钟后△PCQ的面积等于△ABC的一半?
点P、Q同时由A、B两点出发,分别沿AC,BC的方向匀速运动,它们的速度都是每秒1cm,____秒钟后△PCQ的面积等于△ABC的一半?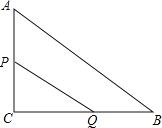
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB//CD.

(1)如图①,若∠ABE=40o,∠BEC=140o,∠ECD=_________o
(2)如图①,试探究∠ABE,∠BEC,∠ECD的关系,并说明理由;
(3)如图②,若CF平分∠ECD,且满足CF∥BE,试探究∠ECD,∠ABE的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
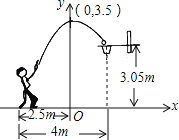
A. 此抛物线的解析式是y=﹣
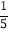 x2+3.5
x2+3.5B. 篮圈中心的坐标是(4,3.05)
C. 此抛物线的顶点坐标是(3.5,0)
D. 篮球出手时离地面的高度是2m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,按下列步骤作图:①以点B为圆心,适当长为半径画弧,与AB,BC分别交于点D,E;②分别以D,E为圆心,大于
 DE的长为半径画弧,两弧交于点P;③作射线BP交AC于点F;④过点F作FG⊥AB于点G.下列结论正确的是( )
DE的长为半径画弧,两弧交于点P;③作射线BP交AC于点F;④过点F作FG⊥AB于点G.下列结论正确的是( )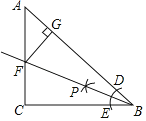
A. CF=FG B. AF=AG C. AF=CF D. AG=FG
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设
 ,
, .
.①如图2,当点在线段BC上移动,则
 ,
, 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;②当点在直线BC上移动,则
 ,
, 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.



相关试题

