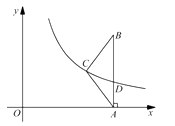
【题目】如图,在 ![]() 中,
中, ![]() ,
, ![]() 轴,垂足为
轴,垂足为 ![]() .反比例函数
.反比例函数 ![]() (
( ![]() )的图像经过点
)的图像经过点 ![]() ,交
,交 ![]() 于点
于点 ![]() .已知
.已知 ![]() ,
, ![]() .
.
(1)若 ![]() ,求
,求 ![]() 的值;
的值;
(2)连接 ![]() ,若
,若 ![]() ,求
,求 ![]() 的长.
的长.
参考答案:
【答案】
(1)
解:过点C作CD⊥AB于E,
因为AC=BC,
所以AE=BE=2,
在Rt△BCE中,CE=![]() ,
,
则点C的横坐标为4-![]() ,
,
即C(![]() ,2)。
,2)。
将点C(![]() ,2)代入y=
,2)代入y=![]() ,得k=5。
,得k=5。
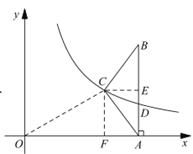
(2)
解:设A点的坐标为(m,0).
因为BD=BC=![]()
所以AD=![]()
则D,C两点的坐标分别为(m,![]() ),(m-
),(m-![]() ,2) .
,2) .
因为点D,C都在y=![]() 的图象上,
的图象上,
所以![]() ,
,
所以m=6
所以点C的坐标为(![]() ,2)
,2)
作CF⊥x轴,垂足为F.在Rt△OCF中,
OC=![]() .
.

【解析】(1)求点C的坐标,过点C作CD⊥AB于E,则AE=BE=2,由勾股定理求出CE,则求得点C的坐标,代入反比例函数即可解得;
(2)求点C的坐标,设A点的坐标为(m,0),由BD=BC=![]() ,可得D的纵坐标为AD=
,可得D的纵坐标为AD=![]() ,则D(m,
,则D(m,![]() ),C(m-
),C(m-![]() ,2) .由点D,C都在y=
,2) .由点D,C都在y=![]() 的图象上,,可求出m的值,即而求出点C的坐标,根据勾股定理即可求OC的长。
的图象上,,可求出m的值,即而求出点C的坐标,根据勾股定理即可求OC的长。
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
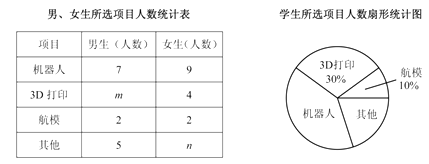
根据以上信息解决下列问题:
(1)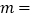 ,
, 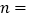 ;
;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ;
;
(3)从选航模项目的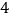 名学生中随机选取
名学生中随机选取 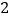 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的 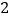 名学生中恰好有
名学生中恰好有 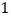 名男生、
名男生、 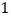 名女生的概率.
名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
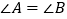 ,
, 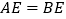 ,点
,点 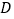 在
在 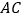 边上,
边上, 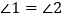 ,
, 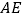 和
和 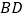 相交于点
相交于点 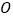 .
.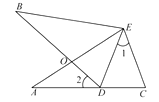
(1)求证: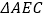 ≌
≌ 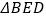 ;
;
(2)若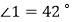 ,求
,求 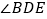 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】4月23日是“世界读书日”,学校开展“让书香溢满校园”读书活动,以提升青少年的阅读兴趣,九年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计,根据所得数据绘制了两幅不完整统计图(每组包括最小值不包括最大值).九年级(1)班每天阅读时间在0.5小时以内的学生占全班人数的8%.根据统计图解答下列问题:
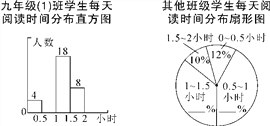
(1)九年级(1)班有 名学生;
(2)补全直方图;
(3)除九年级(1)班外,九年级其他班级每天阅读时间在1~1.5小时的学生有165人,请你补全扇形统计图;
(4)求该年级每天阅读时间不少于1小时的学生有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点
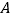 出发,在矩形
出发,在矩形 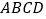 边上沿着
边上沿着 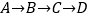 的方向匀速移动,到达点
的方向匀速移动,到达点 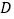 时停止移动.已知机器人的速度为
时停止移动.已知机器人的速度为 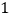 个单位长度/
个单位长度/ 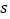 ,移动至拐角处调整方向需要
,移动至拐角处调整方向需要 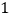
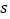 (即在
(即在 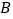 、
、 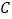 处拐弯时分别用时
处拐弯时分别用时 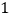
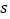 ).设机器人所用时间为
).设机器人所用时间为 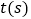 时,其所在位置用点
时,其所在位置用点 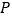 表示,
表示, 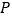 到对角线
到对角线 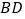 的距离(即垂线段
的距离(即垂线段 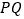 的长)为
的长)为 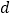 个单位长度,其中
个单位长度,其中 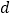 与
与 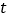 的函数图像如图②所示.
的函数图像如图②所示.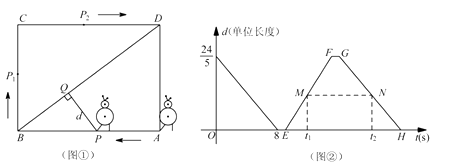
(1)求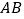 、
、 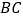 的长;
的长;
(2)如图②,点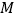 、
、 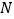 分别在线段
分别在线段 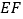 、
、 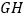 上,线段
上,线段 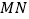 平行于横轴,
平行于横轴, 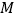 、
、 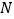 的横坐标分别为
的横坐标分别为 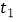 、
、 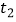 .设机器人用了
.设机器人用了 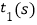 到达点
到达点 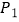 处,用了
处,用了 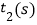 到达点
到达点 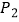 处(见图①).若
处(见图①).若 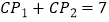 ,求
,求 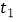 、
、 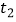 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某教研机构为了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查.依据相关数据绘制成如图所示的不完整的统计图表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表

类别
人数
占总人数比例
重视
a
0.3
一般
57
0.38
不重视
b
c
说不清楚
9
0.06
(1)求样本容量及表格中a,b,c的值,并补全统计图.
(2)若该校共有初中生2 300名,请估计该校“不重视阅读数学教科书”的初中生人数.
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式或不等式组,并把它们的解集在数轴上表示出来.
(1)5x+15>4x-13; (2)
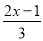 ≤
≤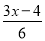 ;
;(3)
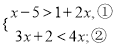 (4)
(4) 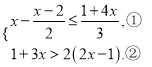
相关试题

